proDA
The goal of proDA is to identify differentially abundant proteins in label-free mass spectrometry data. The main challenge of this data are the many missing values. The missing values don’t occur randomly but especially at low intensities. This means that they cannot just be ignored. Existing methods have mostly focused on replacing the missing values with some reasonable number (“imputation”) and then run classical methods. But imputation is problematic because it obscures the amount of available information. Which in turn can lead to over-confident predictions.
proDA on the other hand does not impute missing values, but constructs a probabilistic dropout model. For each sample it fits a sigmoidal dropout curve. This information can then be used to infer means across samples and the associated uncertainty, without the intermediate imputation step. proDA supports full linear models with variance and location moderation.
For full details, please see our preprint:
Constantin Ahlmann-Eltze and Simon Anders: proDA: Probabilistic Dropout Analysis for Identifying Differentially Abundant Proteins in Label-Free Mass Spectrometry. biorXiv 661496 (Jun 2019)
Installation
proDA is implemented as an R package.
You can install it from Bioconductor by typing the following commands into R:
if(!requireNamespace("BiocManager", quietly = TRUE))
install.packages("BiocManager")
BiocManager::install("proDA")To get the latest development version from GitHub, you can use the devtools package:
The pkgdown documentation for the package is available on https://const-ae.github.io/proDA/reference.
In the following section, I will give a very brief overview on the main functionality of the proDA package, aimed at experienced R users. New users are advised to skip this “quickstart” and to go directly to section 1.3, where I give a complete walkthrough and explain in detail, what steps are necessary for the analysis of label-free mass spectrometry data.
Quickstart
The three steps that are necessary to analyze the data are
- Load the data (see vignette on loading MaxQuant output files)
- Fit the probabilistic dropout model (
proDA()) - Test in which proteins the coefficients of the model differ (
test_diff())
# Load the package
library(proDA)
# Generate some dataset with known structure
syn_dataset <- generate_synthetic_data(n_proteins = 100, n_conditions = 2)
# The abundance matrix
syn_dataset$Y[1:5, ]
#> Condition_1-1 Condition_1-2 Condition_1-3 Condition_2-1 Condition_2-2 Condition_2-3
#> protein_1 NA NA 18.88592 NA 18.72059 20.06119
#> protein_2 21.37123 20.53557 18.83239 20.41027 21.73266 21.16719
#> protein_3 NA 18.77742 18.98681 NA NA 19.20291
#> protein_4 25.44209 25.15151 25.38142 25.22754 24.95229 24.97185
#> protein_5 23.46724 23.15808 23.21357 23.29562 23.25999 23.57925
# Assignment of the samples to the two conditions
syn_dataset$groups
#> [1] Condition_1 Condition_1 Condition_1 Condition_2 Condition_2 Condition_2
#> Levels: Condition_1 Condition_2
# Fit the probabilistic dropout model
fit <- proDA(syn_dataset$Y, design = syn_dataset$groups)
# Identify which proteins differ between Condition 1 and 2
test_diff(fit, `Condition_1` - `Condition_2`, sort_by = "pval", n_max = 5)
#> name pval adj_pval diff t_statistic se df avg_abundance n_approx
#> 96 protein_96 2.480632e-06 0.0002480632 8.617917 39.39412 0.2187615 4 22.16131 4.022503
#> 95 protein_95 1.025837e-05 0.0005129184 -4.839748 -27.59434 0.1753892 4 21.18996 6.000000
#> 91 protein_91 5.279731e-05 0.0017599104 -4.172440 -18.26958 0.2283818 4 19.09951 4.014839
#> 98 protein_98 2.364378e-04 0.0047851432 4.351147 12.48889 0.3484013 4 21.64483 6.000000
#> 100 protein_100 2.392572e-04 0.0047851432 2.494872 12.45115 0.2003729 4 21.32955 4.954439
#> n_obs
#> 96 4
#> 95 6
#> 91 4
#> 98 6
#> 100 5Other helpful functions for quality control are median_normalization() and dist_approx().
proDA Walkthrough
proDA is an R package that implements a powerful probabilistic dropout model to identify differentially abundant proteins. The package was specifically designed for label-free mass spectrometry data and in particular how to handle the many many missing values.
But all this is useless if you cannot load your data and get it into a shape that is useable. In the next section, I will explain how to load the abundance matrix and bring it into a useful form. The steps that I will go through are
- Load the
proteinGroups.txtMaxQuant output table - Extract the intensity columns and create the abundance matrix
- Replace the zeros with
NAs and take thelog2()of the data - Normalize the data using
median_normalization() - Inspect sample structure with a heatmap of the distance matrix (
dist_approx()) - Fit the probabilistic dropout model with
proDA() - Identify differentially abundant proteins with
test_diff()
Load Data
I will now demonstrate how to load a MaxQuant output file. For more information about other approaches for loading the data, please take a look at the vignette on loading data.
MaxQuant is one of the most popular tools for handling raw MS data. It produces a number of files. The important file that contains the protein intensities is called proteinGroups.txt. It is a large table with detailed information about the identification and quantification process for each protein group (which I will from now on just call “protein”).
This package comes with an example proteinGroups.txt file, located in the package folder. The file contains the reduced output from an experiment studying the different DHHCs in Drosophila melanogaster.
system.file("extdata/proteinGroups.txt", package = "proDA", mustWork = TRUE)
#> [1] "/Users/ahlmanne/Library/R/3.6/library/proDA/extdata/proteinGroups.txt"In this example, I will use the base R functions to load the data, because they don’t require any additional dependencies.
# Load the table into memory
maxquant_protein_table <- read.delim(
system.file("extdata/proteinGroups.txt", package = "proDA", mustWork = TRUE),
stringsAsFactors = FALSE
)As I have mentioned, the table contains a lot of information (359 columns!!), but we are first of all interested in the columns which contain the measured intensities.
# I use a regular expression (regex) to select the intensity columns
intensity_colnames <- grep("^LFQ\\.intensity\\.", colnames(maxquant_protein_table), value=TRUE)
head(intensity_colnames)
#> [1] "LFQ.intensity.CG1407.01" "LFQ.intensity.CG1407.02" "LFQ.intensity.CG1407.03"
#> [4] "LFQ.intensity.CG4676.01" "LFQ.intensity.CG4676.02" "LFQ.intensity.CG4676.03"
# Create the intensity matrix
abundance_matrix <- as.matrix(maxquant_protein_table[, intensity_colnames])
# Adapt column and row maxquant_protein_table
colnames(abundance_matrix) <- sub("^LFQ\\.intensity\\.", "", intensity_colnames)
rownames(abundance_matrix) <- maxquant_protein_table$Protein.IDs
# Print some rows of the matrix with short names so they fit on the screen
abundance_matrix[46:48, 1:6]
#> CG1407.01 CG1407.02 CG1407.03 CG4676.01 CG4676.02 CG4676.03
#> A0A0B4K6W1;P08970 713400 845440 0 0 1032600 0
#> A0A0B4K6W2;A0A0B4K7S0;P55824-3;P55824 5018800 4429500 2667200 0 8780200 1395800
#> A0A0B4K6X7;A1Z8J0 0 0 0 0 0 0After extracting the bits from the table we most care about, we will have to modify it.
Firstly, MaxQuant codes missing values as 0. This is misleading, because the actual abundance probably was not zero, but just some value too small to be detected by the mass spectrometer. Accordingly, I will replace all 0 with NA.
Secondly, the raw intensity values have a linear mean-variance relation. This is undesirable, because a change of x units can be a large shift if the mean is small or irrelevant if the mean is large. Luckily, to make the mean and variance independent, we can just log the intensities. Now a change of x units is as significant for highly abundant proteins, as it is for low abundant ones.
abundance_matrix[abundance_matrix == 0] <- NA
abundance_matrix <- log2(abundance_matrix)
abundance_matrix[46:48, 1:6]
#> CG1407.01 CG1407.02 CG1407.03 CG4676.01 CG4676.02 CG4676.03
#> A0A0B4K6W1;P08970 19.44435 19.68934 NA NA 19.97785 NA
#> A0A0B4K6W2;A0A0B4K7S0;P55824-3;P55824 22.25891 22.07871 21.34689 NA 23.06582 20.41266
#> A0A0B4K6X7;A1Z8J0 NA NA NA NA NA NAQuality Control
Quality control (QC) is essential for a successful bioinformatics analysis, because any dataset shows some unwanted variation or could even contain more serious error like for example a sample swap.
Often we start with normalizing the data to remove potential sample specific effects. But already this step is challenging, because the missing values cannot easily be corrected for. Thus, a first helpful plot is to look how many missing values are in each sample.
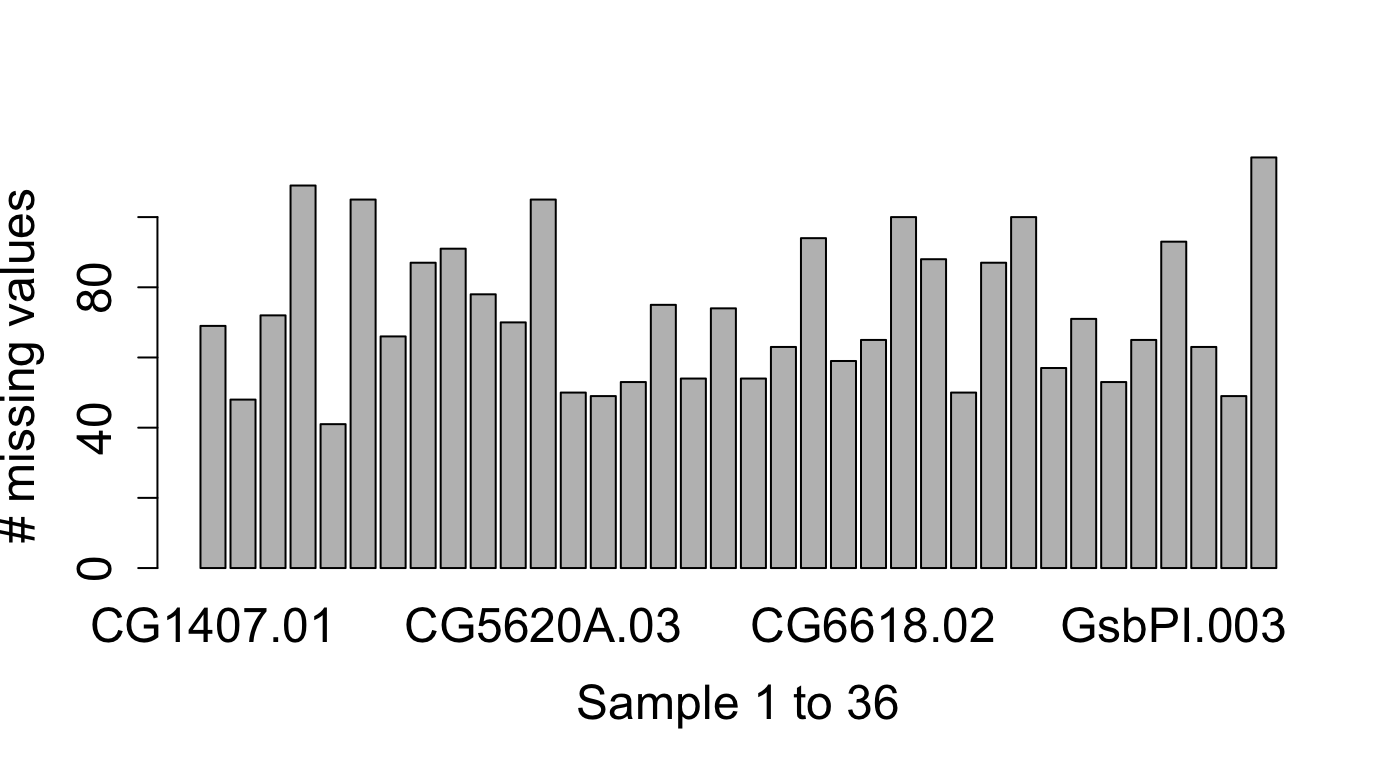
We can see that the number of missing values differs substantially between samples (between 30% and 90%) in this dataset. If we take a look at the intensity distribution for each sample, we see that they differ substantially as well.
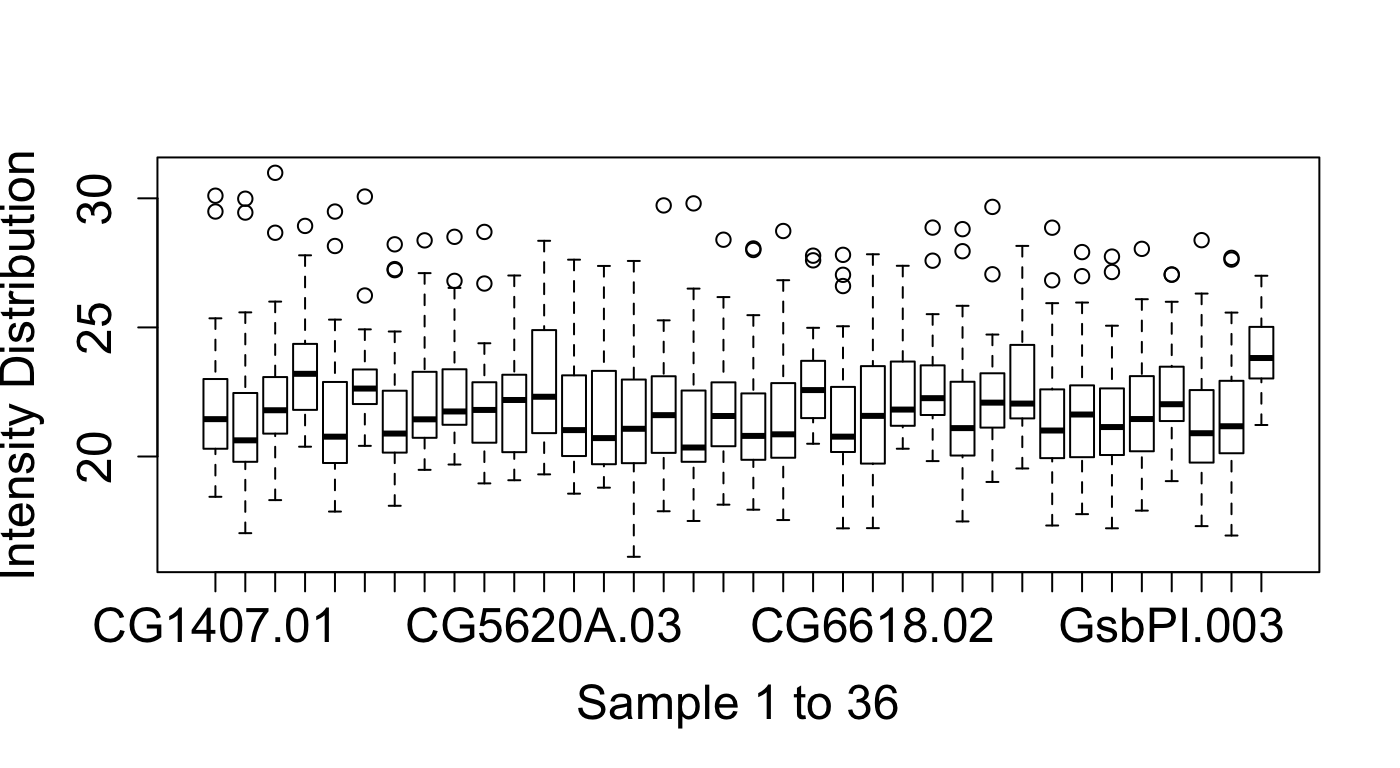
Note that, the intensity distribution is shifted upwards for samples which also have a large number of missing values (for example the last one). This agrees with our idea that small values are more likely to be missing. On the other hand, this also demonstrates why normalization methods such as quantile normalization, which distort the data until all the distributions are equal, are problematic. I will apply the more “conservative” median normalization, which ignores the missing values and transforms the values so that the median difference between the sample and average across all other samples is zero.
An important tool to identify sample swaps and outliers in the dataset is to look at the sample distance matrix. It shows the distances of samples A to B, A to C, B to C and so on.
The base R dist() function can not handle input data that contains missing values, so we might be tempted to just replace the missing values with some realistic numbers and calculate the distance on the completed dataset. But choosing a good replacement value is challenging and can also be misleading because the samples with many missing values would be considered too close.
Instead proDA provides the dist_approx() function that takes either a fitted model (ie. the output from proDA()) or a simple matrix (for which it internally calls proDA()) and estimates the expected distance without imputing the missing values. In addition, it reports the associated uncertainty with every estimate. The estimates for samples with many missing values will be uncertain, allowing the data analyst to discount them.
dist_approx() returns two elements the mean of the estimate and the associated sd. In the next step I will plot the heatmap for three different conditions, adding the 95% confidence interval as text to each cell.
# This chunk only works if pheatmap is installed
# install.packages("pheatmap")
sel <- c(1:3, # CG1407
7:9, # CG59163
22:24)# CG6618
plot_mat <- as.matrix(da$mean)[sel, sel]
# Remove diagonal elements, so that the colorscale is not distorted
plot_mat[diag(9) == 1] <- NA
# 95% conf interval is approx `sd * 1.96`
uncertainty <- matrix(paste0(" ± ",round(as.matrix(da$sd * 1.96)[sel, sel], 1)), nrow=9)
pheatmap::pheatmap(plot_mat,
cluster_rows = FALSE, cluster_cols = FALSE,
display_numbers= uncertainty,
number_color = "black")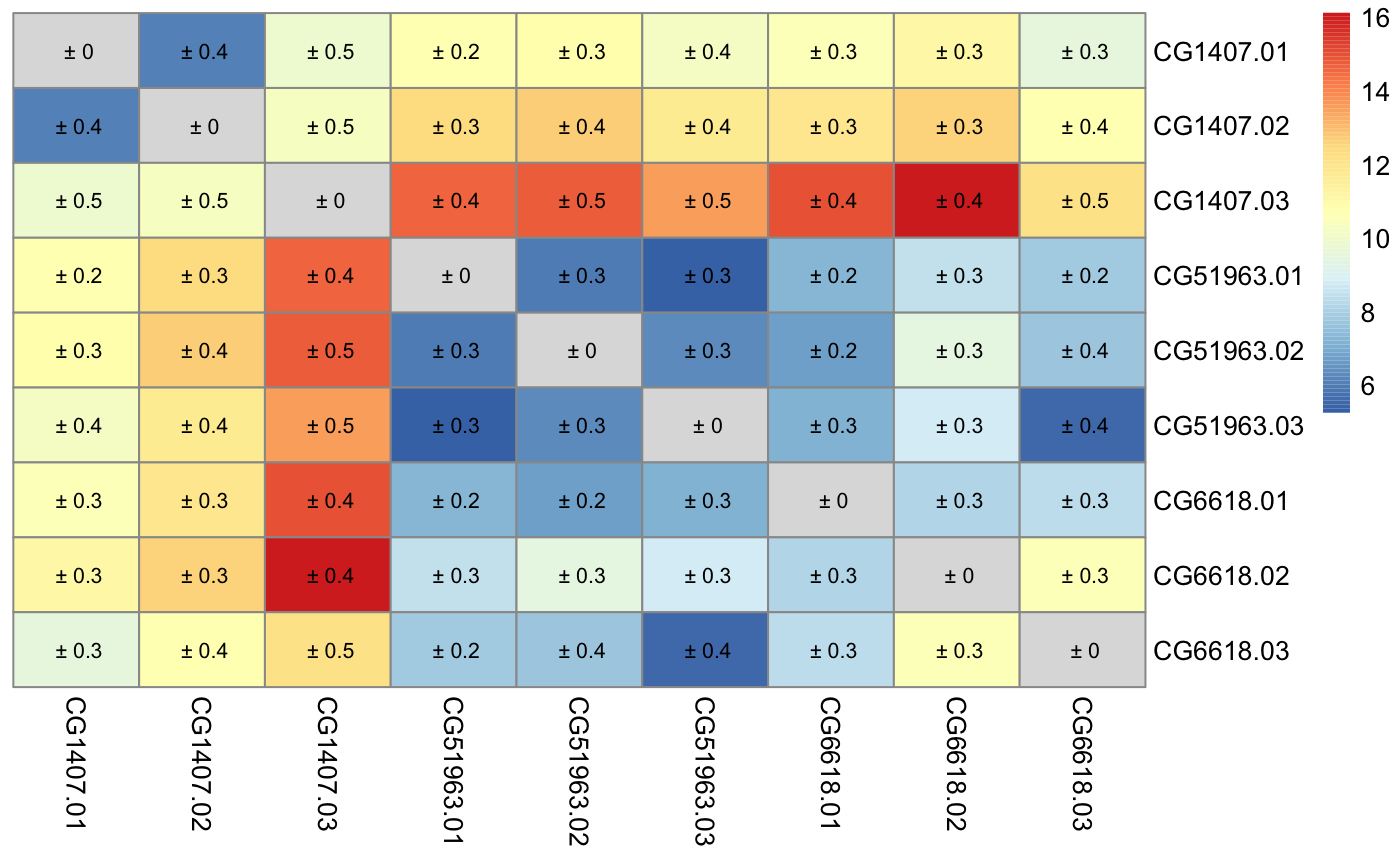
Fit the Probabilistic Dropout Model
In the next step, we will fit the actual linear probabilistic dropout model to the normalized data. But before we start, I will create a data.frame that contains some additional information on each sample, in particular to which condition that sample belongs.
# The best way to create this data.frame depends on the column naming scheme
sample_info_df <- data.frame(name = colnames(normalized_abundance_matrix),
stringsAsFactors = FALSE)
sample_info_df$condition <- substr(sample_info_df$name, 1, nchar(sample_info_df$name) - 3)
sample_info_df$replicate <- as.numeric(
substr(sample_info_df$name, nchar(sample_info_df$name) - 1, 20)
)
sample_info_df
#> name condition replicate
#> 1 CG1407.01 CG1407 1
#> 2 CG1407.02 CG1407 2
#> 3 CG1407.03 CG1407 3
#> 4 CG4676.01 CG4676 1
#> 5 CG4676.02 CG4676 2
#> 6 CG4676.03 CG4676 3
#> 7 CG51963.01 CG51963 1
#> 8 CG51963.02 CG51963 2
#> 9 CG51963.03 CG51963 3
#> 10 CG5620A.01 CG5620A 1
#> 11 CG5620A.02 CG5620A 2
#> 12 CG5620A.03 CG5620A 3
#> 13 CG5620B.01 CG5620B 1
#> 14 CG5620B.02 CG5620B 2
#> 15 CG5620B.03 CG5620B 3
#> 16 CG5880.01 CG5880 1
#> 17 CG5880.02 CG5880 2
#> 18 CG5880.03 CG5880 3
#> 19 CG6017.01 CG6017 1
#> 20 CG6017.02 CG6017 2
#> 21 CG6017.03 CG6017 3
#> 22 CG6618.01 CG6618 1
#> 23 CG6618.02 CG6618 2
#> 24 CG6618.03 CG6618 3
#> 25 CG6627.01 CG6627 1
#> 26 CG6627.02 CG6627 2
#> 27 CG6627.03 CG6627 3
#> 28 CG8314.01 CG8314 1
#> 29 CG8314.02 CG8314 2
#> 30 CG8314.03 CG8314 3
#> 31 GsbPI.001 GsbPI. 1
#> 32 GsbPI.002 GsbPI. 2
#> 33 GsbPI.003 GsbPI. 3
#> 34 S2R.01 S2R 1
#> 35 S2R.02 S2R 2
#> 36 S2R.03 S2R 3Now we can call the proDA() function to actually fit the model. We specify the design using the formula notation, referencing the condition column in the sample_info_df data.frame that we have just created. In addition, I specify that I want to use the S2R condition as the reference because I know that it was the negative control and this way automatically all coefficients measure how much each condition differs from the negative control.
fit <- proDA(normalized_abundance_matrix, design = ~ condition,
col_data = sample_info_df, reference_level = "S2R")
fit
#> Parameters of the probabilistic dropout model
#>
#> The dataset contains 36 samples and 122 proteins
#> 59.7% of the values are missing
#>
#> Experimental design: y~condition
#> The model has successfully converged.
#>
#> The inferred parameters are:
#> location_prior_mean: 19.5
#> location_prior_scale: 8.37
#> location_prior_df: 3
#> variance_prior_scale: 0.283
#> variance_prior_df: 1.64
#> dropout_curve_position: 19.9, 19, 20.1, 22.8, ...
#> dropout_curve_scale: -0.816, -0.601, -1.02, -1.3, ...The proDAFit object prints a number of useful information about the convergence of the model, the size of the dataset, the number of missing values, and the inferred hyper parameters.
To make it easy to find available methods on the proDAFit object, the $-operator is overloaded and shows a list of possible functions:

Screenshot from Rstudio suggesting the available functions
# Equivalent to feature_parameters(fit)
fit$feature_parameters
#> n_approx
#> Q8IP47;Q9VJP8;Q9V435;A0A023GPQ3;Q2PDT6;Q7K540 12.00100
#> A0A023GPV6;A8JV04;Q7YU03 12.00100
#> A0A023GQA5;P24156 19.27983
#> Q1RKY1;A0A0B4LG19;A0A0B4J401;B7YZL2;A1ZBH5;B7YZL7;B7YZL6;Q7YTZ4;B7YZL5;B7YZL8;Q0E919;B7YZL1;B7YZL3 12.00100
#> A0A0B4JD00;A8DY69;I0E2I4;A0A0B4JCQ5;Q8SXP0;E5DK16;A0A0B4JD31;A0A0B4JCS1;A0A0B4JD27 17.39307
#> A0A0B4JCT8;Q9V780 12.00100
#> A0A0B4LHQ4;A0A0B4JD62;A0A0B4JDB5;A0A0B4LGQ5;A0A0B4JCW5;A0A0B4JCV6;A0A0B4LGR2;A0A0B4JDA1;Q9VN58 12.00100
#> A0A0B4JCW4;Q9VHJ8;Q95U38 28.92211
#> Q9VDV4;A0A0B4JCY1;Q8IN71;A0A0B4KGH4 12.00100
#> A0A0B4JCY6;Q7KSF4;A0A0B4KHN1;A0A0B4KGT8;Q9VEN1;A0A0B4KGB3;A4V310;B7Z0L2;Q9VEN1-2 12.00100
#> E1JIU2;Q9VCQ0;A0A0B4JCZ2;A8JR87;A0A0B4KH86 12.00100
#> A0A0B4LEY5;A1Z7T2;A0A0B4JD07;A0A0B4K6U3;A0A0B4K727;A0A0B4LF03;A0A0B4LEI8;E1JH15;A0A0B4JD60;A1Z7T1;A1Z7T3;A0A0B4LFX2;A8DY76;A1Z7T0;A1Z7T0-2;A1Z7T4 13.26599
#> A0A0B4JD11;Q9NJH0 34.50696
#> A0A0B4KHW7;Q961V3;A0A0B4KHJ3;A0A0B4KHF5;A0A0B4JD23;Q7KRU0;Q8IMI0;A0A0B4JDE3;Q9VA53 12.00100
#> A0A0B4JD46;Q8T8R1 33.97973
#> A0A0B4JD48;Q95029-2;Q95029 29.09390
#> A0A0B4JD95;Q59E58;A0A0B4JD57;Q59E59;A0A0B4K7Q4;Q99323-2;Q99323-4;Q99323-1;Q99323 21.16573
#> A0A0B4JDA0;Q9VF03 14.58983
#> A0A0B4JDC3;Q9VGU5 12.00100
#> A0A0B4JDG2;Q9I7I8;A0A0B4JDD8;B7Z0M9;Q7KSB3;A0A0B4JCZ0;Q8IN56;Q8IN55 34.87011
#> A0A0B4JDG5;Q8IMZ9 19.68847
#> Q9VNF8;A0A0B4K6T4;A0A0B4K5Z8 14.13399
#> A0A0B4K603;A0A0B4K6V2;A0A0B4KF90;A0A0B4K631;A0A0B4KGC6;B7Z0U7;A0A0B4KFE2;E1JJ78;Q9VI75 12.00100
#> Q7KNC5;Q8MSQ5;Q8IPN9;Q9VNA1;Q0KIB9;A0A0B4K620;B7Z0T3;Q9VNA2;A0A0B4K6S8;A4V2F2;Q4ABH3;A0A0B4K699;A0A0B4KG49;B7Z0T6;Q8IPN8;A0A0B4KF88;Q8IPN6;Q7KTR7;Q7KTR8 13.52792
#> Q9VEZ3;E1JIM4;A0A0B4K664;A0A0B4K700 17.49006
#> Q8INB6;Q86BR9;Q86NK8;Q4AB31;A0A0B4K7C4;A0A0B4K697;A0A0B4KHL4;Q8IHB0 31.78235
#> A0A0B4K6B8;A0A0B4K7A6;Q86B87-21;Q86B87-19;Q86B87-20;Q86B87-18;Q86B87-17;Q86B87-16;Q86B87-29;Q86B87-28;Q86B87-15;Q86B87-27;Q86B87-23;Q86B87-14;Q86B87-13;Q86B87-31;Q86B87-12;Q86B87-11;Q86B87-10;Q86B87-24;Q86B87-22;Q86B87-25;Q86B87-9;Q86B87-8;Q86B87-7;Q86B87-30;Q86B87-6;Q86B87-5;Q86B87-4;Q86B87-3;Q86B87-2;Q86B87;Q86B87-26 23.49625
#> A0A0B4K6D2;Q9VH95 28.98317
#> A0A0B4K6S1;A0A0B4K6F4;Q8SZN9;E0R905;Q7KSP5;A0A0B4KGA3 12.00100
#> Q9VC62;A0A0B4KGU9;Q7KS16;A0A0B4K6F9 12.00100
#> A0A0B4K6G6;Q9VG05 36.00000
#> A0A0B4KHY2;A0A0B4K784;A0A0B4K7L2;E1JIZ1;A0A0B4KI37;E1JIZ2;A0A0B4K6M4;A0A0B4K6I1;A0A0B4K7W1;E1JIZ0;Q7KRY7-3;Q7KRY7-5;Q7KRY7-8;Q7KRY7-2;Q7KRY7-9;Q7KRY7;Q7KRY7-7;Q7KRY7-10;A0A0B4KHN3;Q7KRY7-6;Q7KRY7-4 12.00100
#> A0A0B4K6J3;Q8IMW5;A0A0C4DHB7;A0A0B4K7S6 12.00100
#> A0A0B4K6K7;Q9VI55;Q9VI55-2 22.56518
#> A0A0B4K6K9;A0A0B4K7Y7;Q9VAW5-1;Q9VAW5;Q9VAW5-2 27.52419
#> Q9VEF7;A0A0B4KHP1;A0A0B4K6L3 12.00100
#> A0A0B4K6L4;Q27601 12.00100
#> A0A0B4K6N1;Q8MLY8 36.00000
#> A0A0B4K6N7;Q9VE34;Q9VE34-2 34.14228
#> Q0E9I5;Q0E9K6;Q0E9K0;Q0E9J7;Q0E9J3;Q0E9I7;Q0E9I1;Q0E9H9;A1Z6X3;A0A0C4DHD8;A0A0B4K7I5;A0A0B4K6Z8;Q0E9K7;Q0E9K2;Q0E9J6;Q0E9J1;Q0E9I3;Q0E9I0;Q0E9H7;Q0E9L9;Q0E9L5;Q0E9L4;Q0E9L8;Q0E9I8;A1Z6X1;A0A0B4K7T6;A0A0B4K6Z3;A0A0B4K6R8;Q0E9M3;Q0E9L1;A0A0B4K7H7;A0A0B4K6Y9;Q0E9L0;A1Z6X2;A0A0B4K827;Q0E9M0;Q0E9K3;Q0E9K1;A0A0B4K7H9;Q0E9K4;Q0E9J8;Q0E9J5;Q0E9J4;Q0E9J2;Q0E9I9;Q0E9I4;Q0E9I2;Q0E9H8;Q0E9H5;Q0E9K9;Q0E9K5;Q0E9J9;Q0E9I6;Q0E9H6;A0A0B4K828;A0A0B4K7T5;Q0E9L7;Q0E9L6;Q0E9L3;Q0E9L2;A0A0B4K7T8;Q0E9M4;Q0E9M2;Q0E9M1;Q0E9J0;A0A0B4K824;A0A0B4K7T4;A0A0B4K6R4;A0A0B4K6Q9;A0A0B4K7I3;A0A0B4K6S2;Q0E9K8;A0A0B4K6Z6;A0A0B4K823;A0A0B4KEF4 11.40295
#> D0Z768;A0A0B4K6T1;A0A0B4K7U5;E1JH02;A0A0B4KFC5;Q86S05-3;Q86S05-2;Q86S05 12.00100
#> A0A0B4K6T7 12.00100
#> A0A0B4K6U2;E1JIJ7;Q8INH9 12.00100
#> A0A0B4K6U6;Q08473-3;Q08473-2;Q08473;Q08473-4 17.64724
#> A0A0B4KHW3;A0A0B4K6V1;Q9VA73-3;Q9VA73-2;Q9VA73 22.13184
#> A0A0B4K6W1;P08970 20.21045
#> A0A0B4K6W2;A0A0B4K7S0;P55824-3;P55824 32.25299
#> A0A0B4K6X7;A1Z8J0 12.00100
#> Q9VHK3;A0A0B4K6Y7;Q8INQ0;A8JQV7;Q9VHK4;B7Z0U1;Q8MQQ3 16.28860
#> A0A0B4LHK4;A0A0B4KHZ8;A0A0B4KHR8;A0A0B4K725;Q9VCA8 33.14310
#> A0A0B4LF93;A1Z928;A1Z927;A0A0B4LF82;Q5U0Y0;A0A0B4K765 12.00100
#> A0A0B4K7A5 36.00000
#> A0A0B4K7G4;P13469 29.01701
#> B7YZQ7;A0A0B4K7G9;O77460 12.00100
#> A0A0B4K7H0;Q7KN74 12.00100
#> Q9VBU7;A0A0B4K7J2 33.88476
#> Q95U21;Q7JQ36;A0A0B4K7J3 17.13504
#> A0A0B4K7K6;Q9VBG6 12.36380
#> A0A0B4K7L0;Q9W252 18.37912
#> A0A0B4K7N2;Q8IN00;D5A7N8;Q9VCX2;Q9VCX1-2;Q9VCX1-4;Q9VCX1-3;Q9VCX1 19.91169
#> Q9VCH4;A0A0B4K7Q6 12.00100
#> A0A0B4K7T7;A1ZAN6;A1ZAN7;A0A0B4LFF8 18.66593
#> A0A0B4KFL2;A1Z9E0;A1Z9D9;A0A0B4K7Y4 12.28946
#> A0A0B4K7Z5;Q7KLV9;Q7KLV9-2 28.86215
#> A0A0B4K812;Q7KNS3 12.00100
#> A0A0B4KFL0;A0A0B4K851;Q4Z8K6-3;Q4Z8K6-2;Q4Z8K6 12.00100
#> A1Z945;A0A0B4K859 31.86834
#> A0A0B4K882;Q7K2Y9 12.00100
#> A0A0B4K8A5;Q9W2F2 27.59466
#> A0A0B4K8A6;Q9W288 12.00100
#> Q5LJQ4;A0A0B4KEH8;A0A0B4KEC2;Q9W5H8 12.00100
#> A0A0B4KED0;Q9W5N2 12.00100
#> A0A0B4KED9;O16844 14.41933
#> A0A0B4KEE4;A1Z6Q1 12.00100
#> E1JGZ7;E1JGZ8;A1Z734;A0A0B4KEE7 12.00100
#> A0A0B4KEI5;Q9V9K7 12.00100
#> Q7JVY0;A0A0B4KEU5;A0A0B4KEJ7 11.50015
#> A1Z9L2;A1Z9L0;A0A0B4KFX4;Q8T076;A0A0B4KEP1;A0A0B4LFC1;A0A0B4KFM5;A0A0B4KF25 18.49791
#> Q5U156;A0A0B4KER0;Q95RL2 19.45324
#> A0A0B4KET0;Q1LZ08 12.99106
#> A0A0B4KFU3;A0A0B4KG58;B7YZJ2;B7YZJ1;E1JH90;A0A0B4KET5;A0A0B4KFA4;E1JH91;A0A0B4KEY4;A1ZAU8-2;A1ZAU8-3;A1ZAU8;A0A0B4KEY6 24.48471
#> Q0E901;A0A0B4KFE6;A0A0B4KEW2 12.00100
#> A0A0B4KFR7;A0A0B4KEW6;Q7KLE5 12.00100
#> A0A0B4KEX0;A1ZAB5 34.95610
#> Q0E993;A0A0B4KF06 25.94325
#> A0A0B4KF46;Q8T0L3 28.61920
#> A0A0B4KG14;A0A0B4KF57;Q9VMY8 23.37489
#> Q7JQL5;A0A0B4KF86 12.00100
#> Q8T0M2;Q0E9C6;A0A0B4KFA3;A8DY97;A8DY98 12.00100
#> Q9VHX9;A0A0B4KFA6 16.73872
#> A0A0B4LGR1;Q9VI14;A0A0B4KFB8;Q6NN86 12.00100
#> A1Z7H3;Q8T3L1;A1Z7H2;A0A0B4KFE4 17.03640
#> A0A0B4KFE5;Q04448-2;Q04448 12.00100
#> A0A0B4KFE9;A1Z8P9 12.00100
#> A0A0B4KGE6;A0A0B4KFH4;P26270 12.00100
#> A0A0B4KFJ7;Q9VHH9 14.25221
#> A0A0B4KFN1;A1Z9R6;A0A0B4KFX9;Q9V727 12.00100
#> A0A0B4KH36;A0A0B4KFQ0;A0A0B4KGR9;Q9VH01;A0A0B4KG50 15.88401
#> A4UZI0;A0A0B4LGK5;A1ZA18;A0A0B4KFR5;A0A0B4KG24 25.95821
#> A0A0B4KFX5;A0A0B4KGG9;A4V2S3;A0A0B4KHB2;A0A0B4KFT4;A0A0B4KGZ7;O46036-2;O46036 18.97891
#> A0A0B4KFU5;Q9V853 10.50293
#> A0A0B4KFW0;Q8T0S6 25.39201
#> Q9VHC4;A0A0B4KFZ2;Q6AWD5 12.00100
#> A0A0B4KFZ9;P84040 27.96731
#> Q7K0G4;A0A0B4KG11;F0JAK5 12.00100
#> A0A0B4KG32;A0A0B4KH26;Q9VH20 11.49544
#> A0A0B4KG41;Q9VES1 12.00100
#> Q9VF92;A0A0B4KG69 12.00100
#> Q9N6D7;A0A0B4KG96 23.14033
#> A0A0B4KHS7;A0A0B4KGE1;Q24151;A0A0B4KGI7;Q24151-2;A0A0B4KHS6;A0A0B4KH10;Q24151-4;Q24151-3 31.04219
#> Q8MQJ5;A0A0B4KGF5;Q9VE69 14.40934
#> Q32KD3;Q7KSW1;Q494I1;A0A0B4KGS8;Q9VHW9;A0A0B4KGF6 25.49768
#> A4V364;A8JR54;Q8IN47;A0A0B4KGK8;Q8IN48;A0A0B4KH21;A0A0B4KH24;A0A0B4KGF9;Q9VDI8;Q7KSA0;A0A0B4KHH8;A0A0B4KHI4;Q95TW4;A0A0B4KGK5;A0A0B4KHT5 12.00100
#> E1JIR4;A0A0B4KGG8;P13607-7;P13607-6;P13607-2;P13607-4;P13607-5;P13607;P13607-3;A8QI34 32.35369
#> A0A0B4KGH0;A0A0B4KHR4;Q9VDW6-2;Q9VDW6-1;Q9VDW6;Q9VDW6-4;Q9VDW6-3;A0A0B4KGB9;Q9VDW3;A0A0B4KHE2;Q7YU29;Q0KI50 12.00100
#> A0A0B4KGI6;Q9VN82;A0A0B4KG43;Q8IPP4;Q8IPP3;A0A0B4KF82;A0A0B4KFK9 26.15976
#> A0A0B4KGJ5;Q9NIV1;A0A0B4KG56 12.00100
#> A0A0B4KGK3;Q95RA8 12.00100
#> A0A0B4KGP8;Q24208;Q24208-2 31.57225
#> Q9VEV1;A0A0B4KGS4 31.92679
#> A0A0B4KGU4;Q9VHP0;M9PBB5;P09052 36.00000
#> A0A0B4KGW0;Q8IMX7-2;A0A0B4J3Z9;Q8IMX7 12.00100
#> df
#> Q8IP47;Q9VJP8;Q9V435;A0A023GPQ3;Q2PDT6;Q7K540 0.0010000
#> A0A023GPV6;A8JV04;Q7YU03 0.0010000
#> A0A023GQA5;P24156 8.9263326
#> Q1RKY1;A0A0B4LG19;A0A0B4J401;B7YZL2;A1ZBH5;B7YZL7;B7YZL6;Q7YTZ4;B7YZL5;B7YZL8;Q0E919;B7YZL1;B7YZL3 0.0010000
#> A0A0B4JD00;A8DY69;I0E2I4;A0A0B4JCQ5;Q8SXP0;E5DK16;A0A0B4JD31;A0A0B4JCS1;A0A0B4JD27 7.0395716
#> A0A0B4JCT8;Q9V780 0.0010000
#> A0A0B4LHQ4;A0A0B4JD62;A0A0B4JDB5;A0A0B4LGQ5;A0A0B4JCW5;A0A0B4JCV6;A0A0B4LGR2;A0A0B4JDA1;Q9VN58 0.0010000
#> A0A0B4JCW4;Q9VHJ8;Q95U38 18.5686168
#> Q9VDV4;A0A0B4JCY1;Q8IN71;A0A0B4KGH4 0.0010000
#> A0A0B4JCY6;Q7KSF4;A0A0B4KHN1;A0A0B4KGT8;Q9VEN1;A0A0B4KGB3;A4V310;B7Z0L2;Q9VEN1-2 0.0010000
#> E1JIU2;Q9VCQ0;A0A0B4JCZ2;A8JR87;A0A0B4KH86 0.0010000
#> A0A0B4LEY5;A1Z7T2;A0A0B4JD07;A0A0B4K6U3;A0A0B4K727;A0A0B4LF03;A0A0B4LEI8;E1JH15;A0A0B4JD60;A1Z7T1;A1Z7T3;A0A0B4LFX2;A8DY76;A1Z7T0;A1Z7T0-2;A1Z7T4 2.9124933
#> A0A0B4JD11;Q9NJH0 24.1534628
#> A0A0B4KHW7;Q961V3;A0A0B4KHJ3;A0A0B4KHF5;A0A0B4JD23;Q7KRU0;Q8IMI0;A0A0B4JDE3;Q9VA53 0.0010000
#> A0A0B4JD46;Q8T8R1 23.6262352
#> A0A0B4JD48;Q95029-2;Q95029 18.7404062
#> A0A0B4JD95;Q59E58;A0A0B4JD57;Q59E59;A0A0B4K7Q4;Q99323-2;Q99323-4;Q99323-1;Q99323 10.8122375
#> A0A0B4JDA0;Q9VF03 4.2363400
#> A0A0B4JDC3;Q9VGU5 0.0010000
#> A0A0B4JDG2;Q9I7I8;A0A0B4JDD8;B7Z0M9;Q7KSB3;A0A0B4JCZ0;Q8IN56;Q8IN55 24.5166162
#> A0A0B4JDG5;Q8IMZ9 9.3349730
#> Q9VNF8;A0A0B4K6T4;A0A0B4K5Z8 3.7804998
#> A0A0B4K603;A0A0B4K6V2;A0A0B4KF90;A0A0B4K631;A0A0B4KGC6;B7Z0U7;A0A0B4KFE2;E1JJ78;Q9VI75 0.0010000
#> Q7KNC5;Q8MSQ5;Q8IPN9;Q9VNA1;Q0KIB9;A0A0B4K620;B7Z0T3;Q9VNA2;A0A0B4K6S8;A4V2F2;Q4ABH3;A0A0B4K699;A0A0B4KG49;B7Z0T6;Q8IPN8;A0A0B4KF88;Q8IPN6;Q7KTR7;Q7KTR8 3.1744279
#> Q9VEZ3;E1JIM4;A0A0B4K664;A0A0B4K700 7.1365651
#> Q8INB6;Q86BR9;Q86NK8;Q4AB31;A0A0B4K7C4;A0A0B4K697;A0A0B4KHL4;Q8IHB0 21.4288583
#> A0A0B4K6B8;A0A0B4K7A6;Q86B87-21;Q86B87-19;Q86B87-20;Q86B87-18;Q86B87-17;Q86B87-16;Q86B87-29;Q86B87-28;Q86B87-15;Q86B87-27;Q86B87-23;Q86B87-14;Q86B87-13;Q86B87-31;Q86B87-12;Q86B87-11;Q86B87-10;Q86B87-24;Q86B87-22;Q86B87-25;Q86B87-9;Q86B87-8;Q86B87-7;Q86B87-30;Q86B87-6;Q86B87-5;Q86B87-4;Q86B87-3;Q86B87-2;Q86B87;Q86B87-26 13.1427542
#> A0A0B4K6D2;Q9VH95 18.6296796
#> A0A0B4K6S1;A0A0B4K6F4;Q8SZN9;E0R905;Q7KSP5;A0A0B4KGA3 0.0010000
#> Q9VC62;A0A0B4KGU9;Q7KS16;A0A0B4K6F9 0.0010000
#> A0A0B4K6G6;Q9VG05 25.6465050
#> A0A0B4KHY2;A0A0B4K784;A0A0B4K7L2;E1JIZ1;A0A0B4KI37;E1JIZ2;A0A0B4K6M4;A0A0B4K6I1;A0A0B4K7W1;E1JIZ0;Q7KRY7-3;Q7KRY7-5;Q7KRY7-8;Q7KRY7-2;Q7KRY7-9;Q7KRY7;Q7KRY7-7;Q7KRY7-10;A0A0B4KHN3;Q7KRY7-6;Q7KRY7-4 0.0010000
#> A0A0B4K6J3;Q8IMW5;A0A0C4DHB7;A0A0B4K7S6 0.0010000
#> A0A0B4K6K7;Q9VI55;Q9VI55-2 12.2116871
#> A0A0B4K6K9;A0A0B4K7Y7;Q9VAW5-1;Q9VAW5;Q9VAW5-2 17.1706969
#> Q9VEF7;A0A0B4KHP1;A0A0B4K6L3 0.0010000
#> A0A0B4K6L4;Q27601 0.0010000
#> A0A0B4K6N1;Q8MLY8 25.6465054
#> A0A0B4K6N7;Q9VE34;Q9VE34-2 23.7887834
#> Q0E9I5;Q0E9K6;Q0E9K0;Q0E9J7;Q0E9J3;Q0E9I7;Q0E9I1;Q0E9H9;A1Z6X3;A0A0C4DHD8;A0A0B4K7I5;A0A0B4K6Z8;Q0E9K7;Q0E9K2;Q0E9J6;Q0E9J1;Q0E9I3;Q0E9I0;Q0E9H7;Q0E9L9;Q0E9L5;Q0E9L4;Q0E9L8;Q0E9I8;A1Z6X1;A0A0B4K7T6;A0A0B4K6Z3;A0A0B4K6R8;Q0E9M3;Q0E9L1;A0A0B4K7H7;A0A0B4K6Y9;Q0E9L0;A1Z6X2;A0A0B4K827;Q0E9M0;Q0E9K3;Q0E9K1;A0A0B4K7H9;Q0E9K4;Q0E9J8;Q0E9J5;Q0E9J4;Q0E9J2;Q0E9I9;Q0E9I4;Q0E9I2;Q0E9H8;Q0E9H5;Q0E9K9;Q0E9K5;Q0E9J9;Q0E9I6;Q0E9H6;A0A0B4K828;A0A0B4K7T5;Q0E9L7;Q0E9L6;Q0E9L3;Q0E9L2;A0A0B4K7T8;Q0E9M4;Q0E9M2;Q0E9M1;Q0E9J0;A0A0B4K824;A0A0B4K7T4;A0A0B4K6R4;A0A0B4K6Q9;A0A0B4K7I3;A0A0B4K6S2;Q0E9K8;A0A0B4K6Z6;A0A0B4K823;A0A0B4KEF4 1.0494597
#> D0Z768;A0A0B4K6T1;A0A0B4K7U5;E1JH02;A0A0B4KFC5;Q86S05-3;Q86S05-2;Q86S05 0.0010000
#> A0A0B4K6T7 0.0010000
#> A0A0B4K6U2;E1JIJ7;Q8INH9 0.0010000
#> A0A0B4K6U6;Q08473-3;Q08473-2;Q08473;Q08473-4 7.2937423
#> A0A0B4KHW3;A0A0B4K6V1;Q9VA73-3;Q9VA73-2;Q9VA73 11.7783479
#> A0A0B4K6W1;P08970 9.8569521
#> A0A0B4K6W2;A0A0B4K7S0;P55824-3;P55824 21.8994998
#> A0A0B4K6X7;A1Z8J0 0.0010000
#> Q9VHK3;A0A0B4K6Y7;Q8INQ0;A8JQV7;Q9VHK4;B7Z0U1;Q8MQQ3 5.9351039
#> A0A0B4LHK4;A0A0B4KHZ8;A0A0B4KHR8;A0A0B4K725;Q9VCA8 22.7896039
#> A0A0B4LF93;A1Z928;A1Z927;A0A0B4LF82;Q5U0Y0;A0A0B4K765 0.0010000
#> A0A0B4K7A5 25.6465050
#> A0A0B4K7G4;P13469 18.6635141
#> B7YZQ7;A0A0B4K7G9;O77460 0.0010000
#> A0A0B4K7H0;Q7KN74 0.0010000
#> Q9VBU7;A0A0B4K7J2 23.5312696
#> Q95U21;Q7JQ36;A0A0B4K7J3 6.7815403
#> A0A0B4K7K6;Q9VBG6 2.0103042
#> A0A0B4K7L0;Q9W252 8.0256263
#> A0A0B4K7N2;Q8IN00;D5A7N8;Q9VCX2;Q9VCX1-2;Q9VCX1-4;Q9VCX1-3;Q9VCX1 9.5581943
#> Q9VCH4;A0A0B4K7Q6 0.0010000
#> A0A0B4K7T7;A1ZAN6;A1ZAN7;A0A0B4LFF8 8.3124398
#> A0A0B4KFL2;A1Z9E0;A1Z9D9;A0A0B4K7Y4 1.9359610
#> A0A0B4K7Z5;Q7KLV9;Q7KLV9-2 18.5086525
#> A0A0B4K812;Q7KNS3 0.0010000
#> A0A0B4KFL0;A0A0B4K851;Q4Z8K6-3;Q4Z8K6-2;Q4Z8K6 0.0010000
#> A1Z945;A0A0B4K859 21.5148426
#> A0A0B4K882;Q7K2Y9 0.0010000
#> A0A0B4K8A5;Q9W2F2 17.2411648
#> A0A0B4K8A6;Q9W288 0.0010000
#> Q5LJQ4;A0A0B4KEH8;A0A0B4KEC2;Q9W5H8 0.0010000
#> A0A0B4KED0;Q9W5N2 0.0010000
#> A0A0B4KED9;O16844 4.0658340
#> A0A0B4KEE4;A1Z6Q1 0.0010000
#> E1JGZ7;E1JGZ8;A1Z734;A0A0B4KEE7 0.0010000
#> A0A0B4KEI5;Q9V9K7 0.0010000
#> Q7JVY0;A0A0B4KEU5;A0A0B4KEJ7 1.1466538
#> A1Z9L2;A1Z9L0;A0A0B4KFX4;Q8T076;A0A0B4KEP1;A0A0B4LFC1;A0A0B4KFM5;A0A0B4KF25 8.1444189
#> Q5U156;A0A0B4KER0;Q95RL2 9.0997439
#> A0A0B4KET0;Q1LZ08 2.6375617
#> A0A0B4KFU3;A0A0B4KG58;B7YZJ2;B7YZJ1;E1JH90;A0A0B4KET5;A0A0B4KFA4;E1JH91;A0A0B4KEY4;A1ZAU8-2;A1ZAU8-3;A1ZAU8;A0A0B4KEY6 14.1312154
#> Q0E901;A0A0B4KFE6;A0A0B4KEW2 0.0010000
#> A0A0B4KFR7;A0A0B4KEW6;Q7KLE5 0.0010000
#> A0A0B4KEX0;A1ZAB5 24.6026067
#> Q0E993;A0A0B4KF06 15.5897573
#> A0A0B4KF46;Q8T0L3 18.2657004
#> A0A0B4KG14;A0A0B4KF57;Q9VMY8 13.0213907
#> Q7JQL5;A0A0B4KF86 0.0010000
#> Q8T0M2;Q0E9C6;A0A0B4KFA3;A8DY97;A8DY98 0.0010000
#> Q9VHX9;A0A0B4KFA6 6.3852222
#> A0A0B4LGR1;Q9VI14;A0A0B4KFB8;Q6NN86 0.0010000
#> A1Z7H3;Q8T3L1;A1Z7H2;A0A0B4KFE4 6.6829043
#> A0A0B4KFE5;Q04448-2;Q04448 0.0010000
#> A0A0B4KFE9;A1Z8P9 0.0010000
#> A0A0B4KGE6;A0A0B4KFH4;P26270 0.0010000
#> A0A0B4KFJ7;Q9VHH9 3.8987193
#> A0A0B4KFN1;A1Z9R6;A0A0B4KFX9;Q9V727 0.0010000
#> A0A0B4KH36;A0A0B4KFQ0;A0A0B4KGR9;Q9VH01;A0A0B4KG50 5.5305196
#> A4UZI0;A0A0B4LGK5;A1ZA18;A0A0B4KFR5;A0A0B4KG24 15.6047171
#> A0A0B4KFX5;A0A0B4KGG9;A4V2S3;A0A0B4KHB2;A0A0B4KFT4;A0A0B4KGZ7;O46036-2;O46036 8.6254145
#> A0A0B4KFU5;Q9V853 0.1494317
#> A0A0B4KFW0;Q8T0S6 15.0385197
#> Q9VHC4;A0A0B4KFZ2;Q6AWD5 0.0010000
#> A0A0B4KFZ9;P84040 17.6138143
#> Q7K0G4;A0A0B4KG11;F0JAK5 0.0010000
#> A0A0B4KG32;A0A0B4KH26;Q9VH20 1.1419438
#> A0A0B4KG41;Q9VES1 0.0010000
#> Q9VF92;A0A0B4KG69 0.0010000
#> Q9N6D7;A0A0B4KG96 12.7868384
#> A0A0B4KHS7;A0A0B4KGE1;Q24151;A0A0B4KGI7;Q24151-2;A0A0B4KHS6;A0A0B4KH10;Q24151-4;Q24151-3 20.6886980
#> Q8MQJ5;A0A0B4KGF5;Q9VE69 4.0558402
#> Q32KD3;Q7KSW1;Q494I1;A0A0B4KGS8;Q9VHW9;A0A0B4KGF6 15.1441885
#> A4V364;A8JR54;Q8IN47;A0A0B4KGK8;Q8IN48;A0A0B4KH21;A0A0B4KH24;A0A0B4KGF9;Q9VDI8;Q7KSA0;A0A0B4KHH8;A0A0B4KHI4;Q95TW4;A0A0B4KGK5;A0A0B4KHT5 0.0010000
#> E1JIR4;A0A0B4KGG8;P13607-7;P13607-6;P13607-2;P13607-4;P13607-5;P13607;P13607-3;A8QI34 22.0001990
#> A0A0B4KGH0;A0A0B4KHR4;Q9VDW6-2;Q9VDW6-1;Q9VDW6;Q9VDW6-4;Q9VDW6-3;A0A0B4KGB9;Q9VDW3;A0A0B4KHE2;Q7YU29;Q0KI50 0.0010000
#> A0A0B4KGI6;Q9VN82;A0A0B4KG43;Q8IPP4;Q8IPP3;A0A0B4KF82;A0A0B4KFK9 15.8062684
#> A0A0B4KGJ5;Q9NIV1;A0A0B4KG56 0.0010000
#> A0A0B4KGK3;Q95RA8 0.0010000
#> A0A0B4KGP8;Q24208;Q24208-2 21.2187519
#> Q9VEV1;A0A0B4KGS4 21.5732947
#> A0A0B4KGU4;Q9VHP0;M9PBB5;P09052 25.6465050
#> A0A0B4KGW0;Q8IMX7-2;A0A0B4J3Z9;Q8IMX7 0.0010000
#> s2
#> Q8IP47;Q9VJP8;Q9V435;A0A023GPQ3;Q2PDT6;Q7K540 3.807898e+03
#> A0A023GPV6;A8JV04;Q7YU03 2.439128e+03
#> A0A023GQA5;P24156 4.073604e+00
#> Q1RKY1;A0A0B4LG19;A0A0B4J401;B7YZL2;A1ZBH5;B7YZL7;B7YZL6;Q7YTZ4;B7YZL5;B7YZL8;Q0E919;B7YZL1;B7YZL3 8.496692e+02
#> A0A0B4JD00;A8DY69;I0E2I4;A0A0B4JCQ5;Q8SXP0;E5DK16;A0A0B4JD31;A0A0B4JCS1;A0A0B4JD27 4.701403e-01
#> A0A0B4JCT8;Q9V780 2.472148e+03
#> A0A0B4LHQ4;A0A0B4JD62;A0A0B4JDB5;A0A0B4LGQ5;A0A0B4JCW5;A0A0B4JCV6;A0A0B4LGR2;A0A0B4JDA1;Q9VN58 2.410154e+03
#> A0A0B4JCW4;Q9VHJ8;Q95U38 2.170330e-01
#> Q9VDV4;A0A0B4JCY1;Q8IN71;A0A0B4KGH4 1.797498e+03
#> A0A0B4JCY6;Q7KSF4;A0A0B4KHN1;A0A0B4KGT8;Q9VEN1;A0A0B4KGB3;A4V310;B7Z0L2;Q9VEN1-2 1.881032e+03
#> E1JIU2;Q9VCQ0;A0A0B4JCZ2;A8JR87;A0A0B4KH86 9.631861e+02
#> A0A0B4LEY5;A1Z7T2;A0A0B4JD07;A0A0B4K6U3;A0A0B4K727;A0A0B4LF03;A0A0B4LEI8;E1JH15;A0A0B4JD60;A1Z7T1;A1Z7T3;A0A0B4LFX2;A8DY76;A1Z7T0;A1Z7T0-2;A1Z7T4 1.942688e-01
#> A0A0B4JD11;Q9NJH0 3.789168e+00
#> A0A0B4KHW7;Q961V3;A0A0B4KHJ3;A0A0B4KHF5;A0A0B4JD23;Q7KRU0;Q8IMI0;A0A0B4JDE3;Q9VA53 2.480854e+03
#> A0A0B4JD46;Q8T8R1 3.536543e-01
#> A0A0B4JD48;Q95029-2;Q95029 8.611330e-01
#> A0A0B4JD95;Q59E58;A0A0B4JD57;Q59E59;A0A0B4K7Q4;Q99323-2;Q99323-4;Q99323-1;Q99323 6.828732e+00
#> A0A0B4JDA0;Q9VF03 1.110489e+00
#> A0A0B4JDC3;Q9VGU5 2.356933e+03
#> A0A0B4JDG2;Q9I7I8;A0A0B4JDD8;B7Z0M9;Q7KSB3;A0A0B4JCZ0;Q8IN56;Q8IN55 6.476134e-01
#> A0A0B4JDG5;Q8IMZ9 2.620182e-01
#> Q9VNF8;A0A0B4K6T4;A0A0B4K5Z8 1.937137e+00
#> A0A0B4K603;A0A0B4K6V2;A0A0B4KF90;A0A0B4K631;A0A0B4KGC6;B7Z0U7;A0A0B4KFE2;E1JJ78;Q9VI75 1.174077e+03
#> Q7KNC5;Q8MSQ5;Q8IPN9;Q9VNA1;Q0KIB9;A0A0B4K620;B7Z0T3;Q9VNA2;A0A0B4K6S8;A4V2F2;Q4ABH3;A0A0B4K699;A0A0B4KG49;B7Z0T6;Q8IPN8;A0A0B4KF88;Q8IPN6;Q7KTR7;Q7KTR8 1.251821e+00
#> Q9VEZ3;E1JIM4;A0A0B4K664;A0A0B4K700 6.146158e-01
#> Q8INB6;Q86BR9;Q86NK8;Q4AB31;A0A0B4K7C4;A0A0B4K697;A0A0B4KHL4;Q8IHB0 1.421814e-01
#> A0A0B4K6B8;A0A0B4K7A6;Q86B87-21;Q86B87-19;Q86B87-20;Q86B87-18;Q86B87-17;Q86B87-16;Q86B87-29;Q86B87-28;Q86B87-15;Q86B87-27;Q86B87-23;Q86B87-14;Q86B87-13;Q86B87-31;Q86B87-12;Q86B87-11;Q86B87-10;Q86B87-24;Q86B87-22;Q86B87-25;Q86B87-9;Q86B87-8;Q86B87-7;Q86B87-30;Q86B87-6;Q86B87-5;Q86B87-4;Q86B87-3;Q86B87-2;Q86B87;Q86B87-26 4.241321e-01
#> A0A0B4K6D2;Q9VH95 1.002540e+00
#> A0A0B4K6S1;A0A0B4K6F4;Q8SZN9;E0R905;Q7KSP5;A0A0B4KGA3 2.404985e+03
#> Q9VC62;A0A0B4KGU9;Q7KS16;A0A0B4K6F9 1.218167e+03
#> A0A0B4K6G6;Q9VG05 7.309998e-01
#> A0A0B4KHY2;A0A0B4K784;A0A0B4K7L2;E1JIZ1;A0A0B4KI37;E1JIZ2;A0A0B4K6M4;A0A0B4K6I1;A0A0B4K7W1;E1JIZ0;Q7KRY7-3;Q7KRY7-5;Q7KRY7-8;Q7KRY7-2;Q7KRY7-9;Q7KRY7;Q7KRY7-7;Q7KRY7-10;A0A0B4KHN3;Q7KRY7-6;Q7KRY7-4 1.846495e+03
#> A0A0B4K6J3;Q8IMW5;A0A0C4DHB7;A0A0B4K7S6 2.434448e+03
#> A0A0B4K6K7;Q9VI55;Q9VI55-2 9.973899e-02
#> A0A0B4K6K9;A0A0B4K7Y7;Q9VAW5-1;Q9VAW5;Q9VAW5-2 2.030341e-01
#> Q9VEF7;A0A0B4KHP1;A0A0B4K6L3 3.130708e+03
#> A0A0B4K6L4;Q27601 2.460622e+03
#> A0A0B4K6N1;Q8MLY8 4.398128e-01
#> A0A0B4K6N7;Q9VE34;Q9VE34-2 4.486060e-01
#> Q0E9I5;Q0E9K6;Q0E9K0;Q0E9J7;Q0E9J3;Q0E9I7;Q0E9I1;Q0E9H9;A1Z6X3;A0A0C4DHD8;A0A0B4K7I5;A0A0B4K6Z8;Q0E9K7;Q0E9K2;Q0E9J6;Q0E9J1;Q0E9I3;Q0E9I0;Q0E9H7;Q0E9L9;Q0E9L5;Q0E9L4;Q0E9L8;Q0E9I8;A1Z6X1;A0A0B4K7T6;A0A0B4K6Z3;A0A0B4K6R8;Q0E9M3;Q0E9L1;A0A0B4K7H7;A0A0B4K6Y9;Q0E9L0;A1Z6X2;A0A0B4K827;Q0E9M0;Q0E9K3;Q0E9K1;A0A0B4K7H9;Q0E9K4;Q0E9J8;Q0E9J5;Q0E9J4;Q0E9J2;Q0E9I9;Q0E9I4;Q0E9I2;Q0E9H8;Q0E9H5;Q0E9K9;Q0E9K5;Q0E9J9;Q0E9I6;Q0E9H6;A0A0B4K828;A0A0B4K7T5;Q0E9L7;Q0E9L6;Q0E9L3;Q0E9L2;A0A0B4K7T8;Q0E9M4;Q0E9M2;Q0E9M1;Q0E9J0;A0A0B4K824;A0A0B4K7T4;A0A0B4K6R4;A0A0B4K6Q9;A0A0B4K7I3;A0A0B4K6S2;Q0E9K8;A0A0B4K6Z6;A0A0B4K823;A0A0B4KEF4 2.689023e+00
#> D0Z768;A0A0B4K6T1;A0A0B4K7U5;E1JH02;A0A0B4KFC5;Q86S05-3;Q86S05-2;Q86S05 1.913650e+03
#> A0A0B4K6T7 4.632439e+03
#> A0A0B4K6U2;E1JIJ7;Q8INH9 2.472990e+03
#> A0A0B4K6U6;Q08473-3;Q08473-2;Q08473;Q08473-4 5.211571e-01
#> A0A0B4KHW3;A0A0B4K6V1;Q9VA73-3;Q9VA73-2;Q9VA73 6.511397e-02
#> A0A0B4K6W1;P08970 7.475960e-02
#> A0A0B4K6W2;A0A0B4K7S0;P55824-3;P55824 6.971220e-01
#> A0A0B4K6X7;A1Z8J0 3.227667e+03
#> Q9VHK3;A0A0B4K6Y7;Q8INQ0;A8JQV7;Q9VHK4;B7Z0U1;Q8MQQ3 9.106838e-01
#> A0A0B4LHK4;A0A0B4KHZ8;A0A0B4KHR8;A0A0B4K725;Q9VCA8 2.468212e-01
#> A0A0B4LF93;A1Z928;A1Z927;A0A0B4LF82;Q5U0Y0;A0A0B4K765 2.432625e+03
#> A0A0B4K7A5 4.282051e-01
#> A0A0B4K7G4;P13469 1.045620e+00
#> B7YZQ7;A0A0B4K7G9;O77460 7.556683e+02
#> A0A0B4K7H0;Q7KN74 1.396603e+03
#> Q9VBU7;A0A0B4K7J2 5.182591e-01
#> Q95U21;Q7JQ36;A0A0B4K7J3 1.280748e-01
#> A0A0B4K7K6;Q9VBG6 2.923375e-01
#> A0A0B4K7L0;Q9W252 1.306831e-01
#> A0A0B4K7N2;Q8IN00;D5A7N8;Q9VCX2;Q9VCX1-2;Q9VCX1-4;Q9VCX1-3;Q9VCX1 2.304108e-01
#> Q9VCH4;A0A0B4K7Q6 9.880839e+04
#> A0A0B4K7T7;A1ZAN6;A1ZAN7;A0A0B4LFF8 3.081843e-01
#> A0A0B4KFL2;A1Z9E0;A1Z9D9;A0A0B4K7Y4 2.335598e+01
#> A0A0B4K7Z5;Q7KLV9;Q7KLV9-2 3.950406e-01
#> A0A0B4K812;Q7KNS3 2.758387e+03
#> A0A0B4KFL0;A0A0B4K851;Q4Z8K6-3;Q4Z8K6-2;Q4Z8K6 3.226711e+03
#> A1Z945;A0A0B4K859 4.515658e-01
#> A0A0B4K882;Q7K2Y9 2.426301e+03
#> A0A0B4K8A5;Q9W2F2 1.120008e-01
#> A0A0B4K8A6;Q9W288 2.443908e+03
#> Q5LJQ4;A0A0B4KEH8;A0A0B4KEC2;Q9W5H8 2.228310e+03
#> A0A0B4KED0;Q9W5N2 2.706163e+03
#> A0A0B4KED9;O16844 7.110483e-01
#> A0A0B4KEE4;A1Z6Q1 1.657407e+03
#> E1JGZ7;E1JGZ8;A1Z734;A0A0B4KEE7 8.152982e+02
#> A0A0B4KEI5;Q9V9K7 2.427000e+03
#> Q7JVY0;A0A0B4KEU5;A0A0B4KEJ7 4.505215e+00
#> A1Z9L2;A1Z9L0;A0A0B4KFX4;Q8T076;A0A0B4KEP1;A0A0B4LFC1;A0A0B4KFM5;A0A0B4KF25 1.962739e-01
#> Q5U156;A0A0B4KER0;Q95RL2 3.755760e-01
#> A0A0B4KET0;Q1LZ08 2.571152e-01
#> A0A0B4KFU3;A0A0B4KG58;B7YZJ2;B7YZJ1;E1JH90;A0A0B4KET5;A0A0B4KFA4;E1JH91;A0A0B4KEY4;A1ZAU8-2;A1ZAU8-3;A1ZAU8;A0A0B4KEY6 4.155369e-01
#> Q0E901;A0A0B4KFE6;A0A0B4KEW2 1.565159e+03
#> A0A0B4KFR7;A0A0B4KEW6;Q7KLE5 2.545943e+03
#> A0A0B4KEX0;A1ZAB5 1.494658e-01
#> Q0E993;A0A0B4KF06 1.813350e+00
#> A0A0B4KF46;Q8T0L3 1.650960e+00
#> A0A0B4KG14;A0A0B4KF57;Q9VMY8 1.994407e-01
#> Q7JQL5;A0A0B4KF86 1.071581e+03
#> Q8T0M2;Q0E9C6;A0A0B4KFA3;A8DY97;A8DY98 2.814665e+03
#> Q9VHX9;A0A0B4KFA6 1.076767e+00
#> A0A0B4LGR1;Q9VI14;A0A0B4KFB8;Q6NN86 1.413052e+03
#> A1Z7H3;Q8T3L1;A1Z7H2;A0A0B4KFE4 2.087935e-01
#> A0A0B4KFE5;Q04448-2;Q04448 2.491378e+03
#> A0A0B4KFE9;A1Z8P9 7.146826e+03
#> A0A0B4KGE6;A0A0B4KFH4;P26270 6.235174e+02
#> A0A0B4KFJ7;Q9VHH9 1.230417e-01
#> A0A0B4KFN1;A1Z9R6;A0A0B4KFX9;Q9V727 2.451474e+03
#> A0A0B4KH36;A0A0B4KFQ0;A0A0B4KGR9;Q9VH01;A0A0B4KG50 2.539969e-01
#> A4UZI0;A0A0B4LGK5;A1ZA18;A0A0B4KFR5;A0A0B4KG24 2.191150e-01
#> A0A0B4KFX5;A0A0B4KGG9;A4V2S3;A0A0B4KHB2;A0A0B4KFT4;A0A0B4KGZ7;O46036-2;O46036 4.198414e-01
#> A0A0B4KFU5;Q9V853 1.418405e+01
#> A0A0B4KFW0;Q8T0S6 1.291343e-01
#> Q9VHC4;A0A0B4KFZ2;Q6AWD5 2.666495e+03
#> A0A0B4KFZ9;P84040 1.683057e+00
#> Q7K0G4;A0A0B4KG11;F0JAK5 2.455446e+03
#> A0A0B4KG32;A0A0B4KH26;Q9VH20 8.043019e-01
#> A0A0B4KG41;Q9VES1 2.416967e+03
#> Q9VF92;A0A0B4KG69 1.900953e+03
#> Q9N6D7;A0A0B4KG96 6.470561e-02
#> A0A0B4KHS7;A0A0B4KGE1;Q24151;A0A0B4KGI7;Q24151-2;A0A0B4KHS6;A0A0B4KH10;Q24151-4;Q24151-3 1.938714e-01
#> Q8MQJ5;A0A0B4KGF5;Q9VE69 1.797467e-01
#> Q32KD3;Q7KSW1;Q494I1;A0A0B4KGS8;Q9VHW9;A0A0B4KGF6 1.610408e-01
#> A4V364;A8JR54;Q8IN47;A0A0B4KGK8;Q8IN48;A0A0B4KH21;A0A0B4KH24;A0A0B4KGF9;Q9VDI8;Q7KSA0;A0A0B4KHH8;A0A0B4KHI4;Q95TW4;A0A0B4KGK5;A0A0B4KHT5 2.451782e+03
#> E1JIR4;A0A0B4KGG8;P13607-7;P13607-6;P13607-2;P13607-4;P13607-5;P13607;P13607-3;A8QI34 5.822209e-01
#> A0A0B4KGH0;A0A0B4KHR4;Q9VDW6-2;Q9VDW6-1;Q9VDW6;Q9VDW6-4;Q9VDW6-3;A0A0B4KGB9;Q9VDW3;A0A0B4KHE2;Q7YU29;Q0KI50 7.200649e+03
#> A0A0B4KGI6;Q9VN82;A0A0B4KG43;Q8IPP4;Q8IPP3;A0A0B4KF82;A0A0B4KFK9 2.162144e+00
#> A0A0B4KGJ5;Q9NIV1;A0A0B4KG56 1.545708e+03
#> A0A0B4KGK3;Q95RA8 2.428308e+03
#> A0A0B4KGP8;Q24208;Q24208-2 6.939202e-01
#> Q9VEV1;A0A0B4KGS4 9.208772e-02
#> A0A0B4KGU4;Q9VHP0;M9PBB5;P09052 6.360842e-01
#> A0A0B4KGW0;Q8IMX7-2;A0A0B4J3Z9;Q8IMX7 2.465431e+03
#> n_obs
#> Q8IP47;Q9VJP8;Q9V435;A0A023GPQ3;Q2PDT6;Q7K540 5
#> A0A023GPV6;A8JV04;Q7YU03 1
#> A0A023GQA5;P24156 14
#> Q1RKY1;A0A0B4LG19;A0A0B4J401;B7YZL2;A1ZBH5;B7YZL7;B7YZL6;Q7YTZ4;B7YZL5;B7YZL8;Q0E919;B7YZL1;B7YZL3 6
#> A0A0B4JD00;A8DY69;I0E2I4;A0A0B4JCQ5;Q8SXP0;E5DK16;A0A0B4JD31;A0A0B4JCS1;A0A0B4JD27 17
#> A0A0B4JCT8;Q9V780 1
#> A0A0B4LHQ4;A0A0B4JD62;A0A0B4JDB5;A0A0B4LGQ5;A0A0B4JCW5;A0A0B4JCV6;A0A0B4LGR2;A0A0B4JDA1;Q9VN58 1
#> A0A0B4JCW4;Q9VHJ8;Q95U38 29
#> Q9VDV4;A0A0B4JCY1;Q8IN71;A0A0B4KGH4 4
#> A0A0B4JCY6;Q7KSF4;A0A0B4KHN1;A0A0B4KGT8;Q9VEN1;A0A0B4KGB3;A4V310;B7Z0L2;Q9VEN1-2 4
#> E1JIU2;Q9VCQ0;A0A0B4JCZ2;A8JR87;A0A0B4KH86 7
#> A0A0B4LEY5;A1Z7T2;A0A0B4JD07;A0A0B4K6U3;A0A0B4K727;A0A0B4LF03;A0A0B4LEI8;E1JH15;A0A0B4JD60;A1Z7T1;A1Z7T3;A0A0B4LFX2;A8DY76;A1Z7T0;A1Z7T0-2;A1Z7T4 13
#> A0A0B4JD11;Q9NJH0 34
#> A0A0B4KHW7;Q961V3;A0A0B4KHJ3;A0A0B4KHF5;A0A0B4JD23;Q7KRU0;Q8IMI0;A0A0B4JDE3;Q9VA53 1
#> A0A0B4JD46;Q8T8R1 34
#> A0A0B4JD48;Q95029-2;Q95029 29
#> A0A0B4JD95;Q59E58;A0A0B4JD57;Q59E59;A0A0B4K7Q4;Q99323-2;Q99323-4;Q99323-1;Q99323 17
#> A0A0B4JDA0;Q9VF03 13
#> A0A0B4JDC3;Q9VGU5 1
#> A0A0B4JDG2;Q9I7I8;A0A0B4JDD8;B7Z0M9;Q7KSB3;A0A0B4JCZ0;Q8IN56;Q8IN55 35
#> A0A0B4JDG5;Q8IMZ9 19
#> Q9VNF8;A0A0B4K6T4;A0A0B4K5Z8 12
#> A0A0B4K603;A0A0B4K6V2;A0A0B4KF90;A0A0B4K631;A0A0B4KGC6;B7Z0U7;A0A0B4KFE2;E1JJ78;Q9VI75 9
#> Q7KNC5;Q8MSQ5;Q8IPN9;Q9VNA1;Q0KIB9;A0A0B4K620;B7Z0T3;Q9VNA2;A0A0B4K6S8;A4V2F2;Q4ABH3;A0A0B4K699;A0A0B4KG49;B7Z0T6;Q8IPN8;A0A0B4KF88;Q8IPN6;Q7KTR7;Q7KTR8 13
#> Q9VEZ3;E1JIM4;A0A0B4K664;A0A0B4K700 17
#> Q8INB6;Q86BR9;Q86NK8;Q4AB31;A0A0B4K7C4;A0A0B4K697;A0A0B4KHL4;Q8IHB0 32
#> A0A0B4K6B8;A0A0B4K7A6;Q86B87-21;Q86B87-19;Q86B87-20;Q86B87-18;Q86B87-17;Q86B87-16;Q86B87-29;Q86B87-28;Q86B87-15;Q86B87-27;Q86B87-23;Q86B87-14;Q86B87-13;Q86B87-31;Q86B87-12;Q86B87-11;Q86B87-10;Q86B87-24;Q86B87-22;Q86B87-25;Q86B87-9;Q86B87-8;Q86B87-7;Q86B87-30;Q86B87-6;Q86B87-5;Q86B87-4;Q86B87-3;Q86B87-2;Q86B87;Q86B87-26 23
#> A0A0B4K6D2;Q9VH95 29
#> A0A0B4K6S1;A0A0B4K6F4;Q8SZN9;E0R905;Q7KSP5;A0A0B4KGA3 1
#> Q9VC62;A0A0B4KGU9;Q7KS16;A0A0B4K6F9 4
#> A0A0B4K6G6;Q9VG05 36
#> A0A0B4KHY2;A0A0B4K784;A0A0B4K7L2;E1JIZ1;A0A0B4KI37;E1JIZ2;A0A0B4K6M4;A0A0B4K6I1;A0A0B4K7W1;E1JIZ0;Q7KRY7-3;Q7KRY7-5;Q7KRY7-8;Q7KRY7-2;Q7KRY7-9;Q7KRY7;Q7KRY7-7;Q7KRY7-10;A0A0B4KHN3;Q7KRY7-6;Q7KRY7-4 2
#> A0A0B4K6J3;Q8IMW5;A0A0C4DHB7;A0A0B4K7S6 1
#> A0A0B4K6K7;Q9VI55;Q9VI55-2 23
#> A0A0B4K6K9;A0A0B4K7Y7;Q9VAW5-1;Q9VAW5;Q9VAW5-2 29
#> Q9VEF7;A0A0B4KHP1;A0A0B4K6L3 1
#> A0A0B4K6L4;Q27601 1
#> A0A0B4K6N1;Q8MLY8 36
#> A0A0B4K6N7;Q9VE34;Q9VE34-2 34
#> Q0E9I5;Q0E9K6;Q0E9K0;Q0E9J7;Q0E9J3;Q0E9I7;Q0E9I1;Q0E9H9;A1Z6X3;A0A0C4DHD8;A0A0B4K7I5;A0A0B4K6Z8;Q0E9K7;Q0E9K2;Q0E9J6;Q0E9J1;Q0E9I3;Q0E9I0;Q0E9H7;Q0E9L9;Q0E9L5;Q0E9L4;Q0E9L8;Q0E9I8;A1Z6X1;A0A0B4K7T6;A0A0B4K6Z3;A0A0B4K6R8;Q0E9M3;Q0E9L1;A0A0B4K7H7;A0A0B4K6Y9;Q0E9L0;A1Z6X2;A0A0B4K827;Q0E9M0;Q0E9K3;Q0E9K1;A0A0B4K7H9;Q0E9K4;Q0E9J8;Q0E9J5;Q0E9J4;Q0E9J2;Q0E9I9;Q0E9I4;Q0E9I2;Q0E9H8;Q0E9H5;Q0E9K9;Q0E9K5;Q0E9J9;Q0E9I6;Q0E9H6;A0A0B4K828;A0A0B4K7T5;Q0E9L7;Q0E9L6;Q0E9L3;Q0E9L2;A0A0B4K7T8;Q0E9M4;Q0E9M2;Q0E9M1;Q0E9J0;A0A0B4K824;A0A0B4K7T4;A0A0B4K6R4;A0A0B4K6Q9;A0A0B4K7I3;A0A0B4K6S2;Q0E9K8;A0A0B4K6Z6;A0A0B4K823;A0A0B4KEF4 10
#> D0Z768;A0A0B4K6T1;A0A0B4K7U5;E1JH02;A0A0B4KFC5;Q86S05-3;Q86S05-2;Q86S05 2
#> A0A0B4K6T7 1
#> A0A0B4K6U2;E1JIJ7;Q8INH9 1
#> A0A0B4K6U6;Q08473-3;Q08473-2;Q08473;Q08473-4 17
#> A0A0B4KHW3;A0A0B4K6V1;Q9VA73-3;Q9VA73-2;Q9VA73 22
#> A0A0B4K6W1;P08970 20
#> A0A0B4K6W2;A0A0B4K7S0;P55824-3;P55824 32
#> A0A0B4K6X7;A1Z8J0 0
#> Q9VHK3;A0A0B4K6Y7;Q8INQ0;A8JQV7;Q9VHK4;B7Z0U1;Q8MQQ3 15
#> A0A0B4LHK4;A0A0B4KHZ8;A0A0B4KHR8;A0A0B4K725;Q9VCA8 33
#> A0A0B4LF93;A1Z928;A1Z927;A0A0B4LF82;Q5U0Y0;A0A0B4K765 1
#> A0A0B4K7A5 36
#> A0A0B4K7G4;P13469 29
#> B7YZQ7;A0A0B4K7G9;O77460 7
#> A0A0B4K7H0;Q7KN74 6
#> Q9VBU7;A0A0B4K7J2 34
#> Q95U21;Q7JQ36;A0A0B4K7J3 17
#> A0A0B4K7K6;Q9VBG6 12
#> A0A0B4K7L0;Q9W252 18
#> A0A0B4K7N2;Q8IN00;D5A7N8;Q9VCX2;Q9VCX1-2;Q9VCX1-4;Q9VCX1-3;Q9VCX1 21
#> Q9VCH4;A0A0B4K7Q6 2
#> A0A0B4K7T7;A1ZAN6;A1ZAN7;A0A0B4LFF8 18
#> A0A0B4KFL2;A1Z9E0;A1Z9D9;A0A0B4K7Y4 8
#> A0A0B4K7Z5;Q7KLV9;Q7KLV9-2 31
#> A0A0B4K812;Q7KNS3 2
#> A0A0B4KFL0;A0A0B4K851;Q4Z8K6-3;Q4Z8K6-2;Q4Z8K6 5
#> A1Z945;A0A0B4K859 32
#> A0A0B4K882;Q7K2Y9 1
#> A0A0B4K8A5;Q9W2F2 29
#> A0A0B4K8A6;Q9W288 1
#> Q5LJQ4;A0A0B4KEH8;A0A0B4KEC2;Q9W5H8 2
#> A0A0B4KED0;Q9W5N2 1
#> A0A0B4KED9;O16844 16
#> A0A0B4KEE4;A1Z6Q1 5
#> E1JGZ7;E1JGZ8;A1Z734;A0A0B4KEE7 7
#> A0A0B4KEI5;Q9V9K7 1
#> Q7JVY0;A0A0B4KEU5;A0A0B4KEJ7 10
#> A1Z9L2;A1Z9L0;A0A0B4KFX4;Q8T076;A0A0B4KEP1;A0A0B4LFC1;A0A0B4KFM5;A0A0B4KF25 18
#> Q5U156;A0A0B4KER0;Q95RL2 19
#> A0A0B4KET0;Q1LZ08 13
#> A0A0B4KFU3;A0A0B4KG58;B7YZJ2;B7YZJ1;E1JH90;A0A0B4KET5;A0A0B4KFA4;E1JH91;A0A0B4KEY4;A1ZAU8-2;A1ZAU8-3;A1ZAU8;A0A0B4KEY6 26
#> Q0E901;A0A0B4KFE6;A0A0B4KEW2 6
#> A0A0B4KFR7;A0A0B4KEW6;Q7KLE5 1
#> A0A0B4KEX0;A1ZAB5 35
#> Q0E993;A0A0B4KF06 25
#> A0A0B4KF46;Q8T0L3 28
#> A0A0B4KG14;A0A0B4KF57;Q9VMY8 24
#> Q7JQL5;A0A0B4KF86 7
#> Q8T0M2;Q0E9C6;A0A0B4KFA3;A8DY97;A8DY98 3
#> Q9VHX9;A0A0B4KFA6 16
#> A0A0B4LGR1;Q9VI14;A0A0B4KFB8;Q6NN86 7
#> A1Z7H3;Q8T3L1;A1Z7H2;A0A0B4KFE4 17
#> A0A0B4KFE5;Q04448-2;Q04448 1
#> A0A0B4KFE9;A1Z8P9 3
#> A0A0B4KGE6;A0A0B4KFH4;P26270 8
#> A0A0B4KFJ7;Q9VHH9 14
#> A0A0B4KFN1;A1Z9R6;A0A0B4KFX9;Q9V727 1
#> A0A0B4KH36;A0A0B4KFQ0;A0A0B4KGR9;Q9VH01;A0A0B4KG50 16
#> A4UZI0;A0A0B4LGK5;A1ZA18;A0A0B4KFR5;A0A0B4KG24 26
#> A0A0B4KFX5;A0A0B4KGG9;A4V2S3;A0A0B4KHB2;A0A0B4KFT4;A0A0B4KGZ7;O46036-2;O46036 18
#> A0A0B4KFU5;Q9V853 11
#> A0A0B4KFW0;Q8T0S6 25
#> Q9VHC4;A0A0B4KFZ2;Q6AWD5 5
#> A0A0B4KFZ9;P84040 27
#> Q7K0G4;A0A0B4KG11;F0JAK5 1
#> A0A0B4KG32;A0A0B4KH26;Q9VH20 11
#> A0A0B4KG41;Q9VES1 1
#> Q9VF92;A0A0B4KG69 2
#> Q9N6D7;A0A0B4KG96 23
#> A0A0B4KHS7;A0A0B4KGE1;Q24151;A0A0B4KGI7;Q24151-2;A0A0B4KHS6;A0A0B4KH10;Q24151-4;Q24151-3 31
#> Q8MQJ5;A0A0B4KGF5;Q9VE69 14
#> Q32KD3;Q7KSW1;Q494I1;A0A0B4KGS8;Q9VHW9;A0A0B4KGF6 25
#> A4V364;A8JR54;Q8IN47;A0A0B4KGK8;Q8IN48;A0A0B4KH21;A0A0B4KH24;A0A0B4KGF9;Q9VDI8;Q7KSA0;A0A0B4KHH8;A0A0B4KHI4;Q95TW4;A0A0B4KGK5;A0A0B4KHT5 1
#> E1JIR4;A0A0B4KGG8;P13607-7;P13607-6;P13607-2;P13607-4;P13607-5;P13607;P13607-3;A8QI34 32
#> A0A0B4KGH0;A0A0B4KHR4;Q9VDW6-2;Q9VDW6-1;Q9VDW6;Q9VDW6-4;Q9VDW6-3;A0A0B4KGB9;Q9VDW3;A0A0B4KHE2;Q7YU29;Q0KI50 1
#> A0A0B4KGI6;Q9VN82;A0A0B4KG43;Q8IPP4;Q8IPP3;A0A0B4KF82;A0A0B4KFK9 24
#> A0A0B4KGJ5;Q9NIV1;A0A0B4KG56 6
#> A0A0B4KGK3;Q95RA8 1
#> A0A0B4KGP8;Q24208;Q24208-2 33
#> Q9VEV1;A0A0B4KGS4 32
#> A0A0B4KGU4;Q9VHP0;M9PBB5;P09052 36
#> A0A0B4KGW0;Q8IMX7-2;A0A0B4J3Z9;Q8IMX7 1Internally the proDAFit object is implemented as a subclass of SummarizedExperiment. This means it can be subsetted, which is for example useful for calculating the distance of a subset of proteins and samples.
# This chunk only works if pheatmap is installed
# install.packages("pheatmap")
pheatmap::pheatmap(dist_approx(fit[1:20, 1:3], by_sample = FALSE)$mean)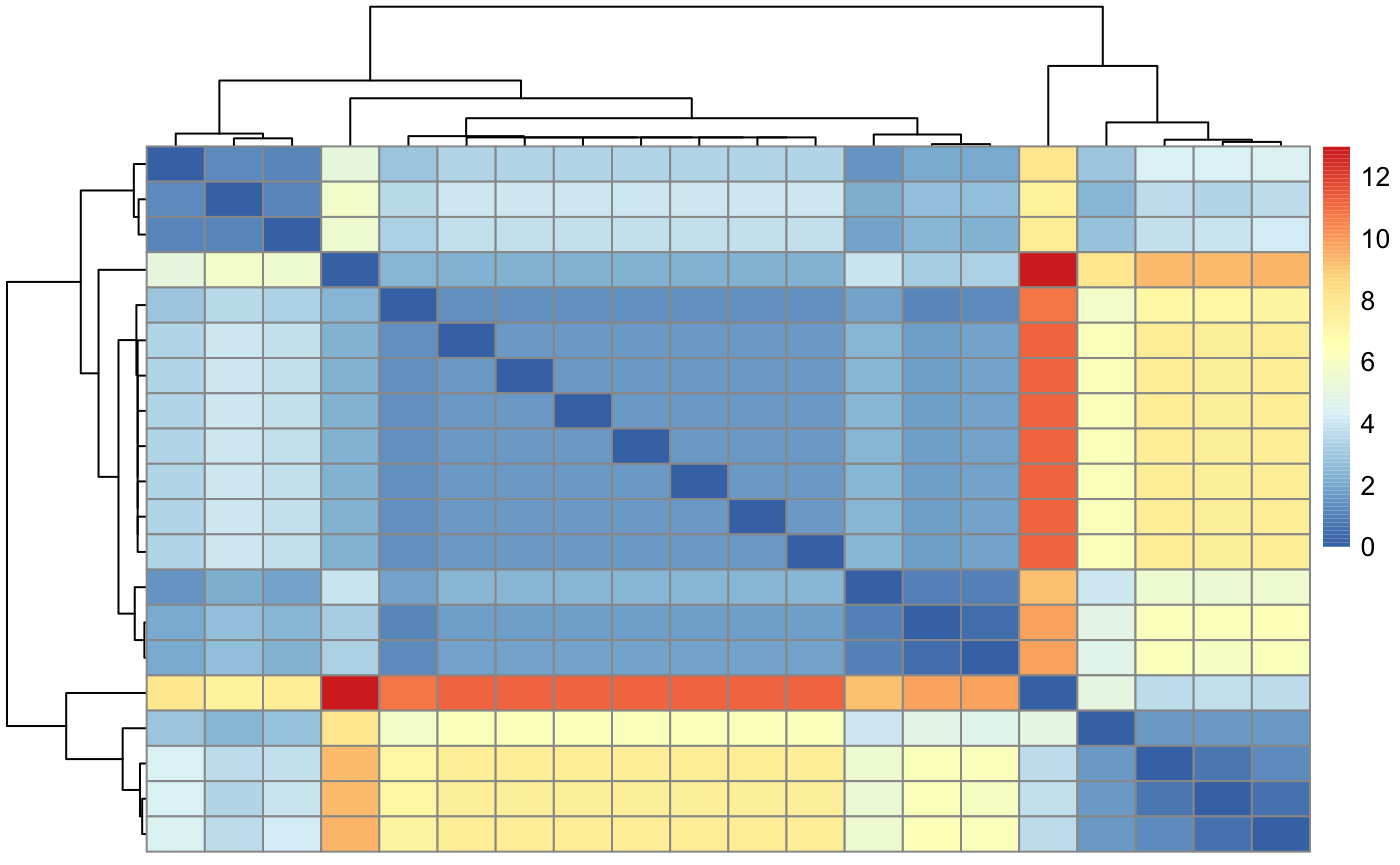
Identify Differential Abundance
Lastly, we will use a Wald test to identify in which proteins a coefficient is significantly different from zero. The test_diff() function takes first the fit object produced by proDA() and a contrast argument. This can either be a string or an expression if we want to test more complex combinations. For example conditionCG1407 - (conditionCG6017 + conditionCG5880) / 2 would test for the difference between CG1407 and the average of CG6017 and CG5880.
Alternatively test_diff() also supports likelihood ratio F-tests. In that case instead of the contrast argument specify the reduced_model argument.
# Test which proteins differ between condition CG1407 and S2R
# S2R is the default contrast, because it was specified as the `reference_level`
test_res <- test_diff(fit, "conditionCG1407")
test_res
#> name
#> 1 Q8IP47;Q9VJP8;Q9V435;A0A023GPQ3;Q2PDT6;Q7K540
#> 2 A0A023GPV6;A8JV04;Q7YU03
#> 3 A0A023GQA5;P24156
#> 4 Q1RKY1;A0A0B4LG19;A0A0B4J401;B7YZL2;A1ZBH5;B7YZL7;B7YZL6;Q7YTZ4;B7YZL5;B7YZL8;Q0E919;B7YZL1;B7YZL3
#> 5 A0A0B4JD00;A8DY69;I0E2I4;A0A0B4JCQ5;Q8SXP0;E5DK16;A0A0B4JD31;A0A0B4JCS1;A0A0B4JD27
#> 6 A0A0B4JCT8;Q9V780
#> 7 A0A0B4LHQ4;A0A0B4JD62;A0A0B4JDB5;A0A0B4LGQ5;A0A0B4JCW5;A0A0B4JCV6;A0A0B4LGR2;A0A0B4JDA1;Q9VN58
#> 8 A0A0B4JCW4;Q9VHJ8;Q95U38
#> 9 Q9VDV4;A0A0B4JCY1;Q8IN71;A0A0B4KGH4
#> 10 A0A0B4JCY6;Q7KSF4;A0A0B4KHN1;A0A0B4KGT8;Q9VEN1;A0A0B4KGB3;A4V310;B7Z0L2;Q9VEN1-2
#> 11 E1JIU2;Q9VCQ0;A0A0B4JCZ2;A8JR87;A0A0B4KH86
#> 12 A0A0B4LEY5;A1Z7T2;A0A0B4JD07;A0A0B4K6U3;A0A0B4K727;A0A0B4LF03;A0A0B4LEI8;E1JH15;A0A0B4JD60;A1Z7T1;A1Z7T3;A0A0B4LFX2;A8DY76;A1Z7T0;A1Z7T0-2;A1Z7T4
#> 13 A0A0B4JD11;Q9NJH0
#> 14 A0A0B4KHW7;Q961V3;A0A0B4KHJ3;A0A0B4KHF5;A0A0B4JD23;Q7KRU0;Q8IMI0;A0A0B4JDE3;Q9VA53
#> 15 A0A0B4JD46;Q8T8R1
#> 16 A0A0B4JD48;Q95029-2;Q95029
#> 17 A0A0B4JD95;Q59E58;A0A0B4JD57;Q59E59;A0A0B4K7Q4;Q99323-2;Q99323-4;Q99323-1;Q99323
#> 18 A0A0B4JDA0;Q9VF03
#> 19 A0A0B4JDC3;Q9VGU5
#> 20 A0A0B4JDG2;Q9I7I8;A0A0B4JDD8;B7Z0M9;Q7KSB3;A0A0B4JCZ0;Q8IN56;Q8IN55
#> 21 A0A0B4JDG5;Q8IMZ9
#> 22 Q9VNF8;A0A0B4K6T4;A0A0B4K5Z8
#> 23 A0A0B4K603;A0A0B4K6V2;A0A0B4KF90;A0A0B4K631;A0A0B4KGC6;B7Z0U7;A0A0B4KFE2;E1JJ78;Q9VI75
#> 24 Q7KNC5;Q8MSQ5;Q8IPN9;Q9VNA1;Q0KIB9;A0A0B4K620;B7Z0T3;Q9VNA2;A0A0B4K6S8;A4V2F2;Q4ABH3;A0A0B4K699;A0A0B4KG49;B7Z0T6;Q8IPN8;A0A0B4KF88;Q8IPN6;Q7KTR7;Q7KTR8
#> 25 Q9VEZ3;E1JIM4;A0A0B4K664;A0A0B4K700
#> 26 Q8INB6;Q86BR9;Q86NK8;Q4AB31;A0A0B4K7C4;A0A0B4K697;A0A0B4KHL4;Q8IHB0
#> 27 A0A0B4K6B8;A0A0B4K7A6;Q86B87-21;Q86B87-19;Q86B87-20;Q86B87-18;Q86B87-17;Q86B87-16;Q86B87-29;Q86B87-28;Q86B87-15;Q86B87-27;Q86B87-23;Q86B87-14;Q86B87-13;Q86B87-31;Q86B87-12;Q86B87-11;Q86B87-10;Q86B87-24;Q86B87-22;Q86B87-25;Q86B87-9;Q86B87-8;Q86B87-7;Q86B87-30;Q86B87-6;Q86B87-5;Q86B87-4;Q86B87-3;Q86B87-2;Q86B87;Q86B87-26
#> 28 A0A0B4K6D2;Q9VH95
#> 29 A0A0B4K6S1;A0A0B4K6F4;Q8SZN9;E0R905;Q7KSP5;A0A0B4KGA3
#> 30 Q9VC62;A0A0B4KGU9;Q7KS16;A0A0B4K6F9
#> 31 A0A0B4K6G6;Q9VG05
#> 32 A0A0B4KHY2;A0A0B4K784;A0A0B4K7L2;E1JIZ1;A0A0B4KI37;E1JIZ2;A0A0B4K6M4;A0A0B4K6I1;A0A0B4K7W1;E1JIZ0;Q7KRY7-3;Q7KRY7-5;Q7KRY7-8;Q7KRY7-2;Q7KRY7-9;Q7KRY7;Q7KRY7-7;Q7KRY7-10;A0A0B4KHN3;Q7KRY7-6;Q7KRY7-4
#> 33 A0A0B4K6J3;Q8IMW5;A0A0C4DHB7;A0A0B4K7S6
#> 34 A0A0B4K6K7;Q9VI55;Q9VI55-2
#> 35 A0A0B4K6K9;A0A0B4K7Y7;Q9VAW5-1;Q9VAW5;Q9VAW5-2
#> 36 Q9VEF7;A0A0B4KHP1;A0A0B4K6L3
#> 37 A0A0B4K6L4;Q27601
#> 38 A0A0B4K6N1;Q8MLY8
#> 39 A0A0B4K6N7;Q9VE34;Q9VE34-2
#> 40 Q0E9I5;Q0E9K6;Q0E9K0;Q0E9J7;Q0E9J3;Q0E9I7;Q0E9I1;Q0E9H9;A1Z6X3;A0A0C4DHD8;A0A0B4K7I5;A0A0B4K6Z8;Q0E9K7;Q0E9K2;Q0E9J6;Q0E9J1;Q0E9I3;Q0E9I0;Q0E9H7;Q0E9L9;Q0E9L5;Q0E9L4;Q0E9L8;Q0E9I8;A1Z6X1;A0A0B4K7T6;A0A0B4K6Z3;A0A0B4K6R8;Q0E9M3;Q0E9L1;A0A0B4K7H7;A0A0B4K6Y9;Q0E9L0;A1Z6X2;A0A0B4K827;Q0E9M0;Q0E9K3;Q0E9K1;A0A0B4K7H9;Q0E9K4;Q0E9J8;Q0E9J5;Q0E9J4;Q0E9J2;Q0E9I9;Q0E9I4;Q0E9I2;Q0E9H8;Q0E9H5;Q0E9K9;Q0E9K5;Q0E9J9;Q0E9I6;Q0E9H6;A0A0B4K828;A0A0B4K7T5;Q0E9L7;Q0E9L6;Q0E9L3;Q0E9L2;A0A0B4K7T8;Q0E9M4;Q0E9M2;Q0E9M1;Q0E9J0;A0A0B4K824;A0A0B4K7T4;A0A0B4K6R4;A0A0B4K6Q9;A0A0B4K7I3;A0A0B4K6S2;Q0E9K8;A0A0B4K6Z6;A0A0B4K823;A0A0B4KEF4
#> 41 D0Z768;A0A0B4K6T1;A0A0B4K7U5;E1JH02;A0A0B4KFC5;Q86S05-3;Q86S05-2;Q86S05
#> 42 A0A0B4K6T7
#> 43 A0A0B4K6U2;E1JIJ7;Q8INH9
#> 44 A0A0B4K6U6;Q08473-3;Q08473-2;Q08473;Q08473-4
#> 45 A0A0B4KHW3;A0A0B4K6V1;Q9VA73-3;Q9VA73-2;Q9VA73
#> 46 A0A0B4K6W1;P08970
#> 47 A0A0B4K6W2;A0A0B4K7S0;P55824-3;P55824
#> 48 A0A0B4K6X7;A1Z8J0
#> 49 Q9VHK3;A0A0B4K6Y7;Q8INQ0;A8JQV7;Q9VHK4;B7Z0U1;Q8MQQ3
#> 50 A0A0B4LHK4;A0A0B4KHZ8;A0A0B4KHR8;A0A0B4K725;Q9VCA8
#> 51 A0A0B4LF93;A1Z928;A1Z927;A0A0B4LF82;Q5U0Y0;A0A0B4K765
#> 52 A0A0B4K7A5
#> 53 A0A0B4K7G4;P13469
#> 54 B7YZQ7;A0A0B4K7G9;O77460
#> 55 A0A0B4K7H0;Q7KN74
#> 56 Q9VBU7;A0A0B4K7J2
#> 57 Q95U21;Q7JQ36;A0A0B4K7J3
#> 58 A0A0B4K7K6;Q9VBG6
#> 59 A0A0B4K7L0;Q9W252
#> 60 A0A0B4K7N2;Q8IN00;D5A7N8;Q9VCX2;Q9VCX1-2;Q9VCX1-4;Q9VCX1-3;Q9VCX1
#> 61 Q9VCH4;A0A0B4K7Q6
#> 62 A0A0B4K7T7;A1ZAN6;A1ZAN7;A0A0B4LFF8
#> 63 A0A0B4KFL2;A1Z9E0;A1Z9D9;A0A0B4K7Y4
#> 64 A0A0B4K7Z5;Q7KLV9;Q7KLV9-2
#> 65 A0A0B4K812;Q7KNS3
#> 66 A0A0B4KFL0;A0A0B4K851;Q4Z8K6-3;Q4Z8K6-2;Q4Z8K6
#> 67 A1Z945;A0A0B4K859
#> 68 A0A0B4K882;Q7K2Y9
#> 69 A0A0B4K8A5;Q9W2F2
#> 70 A0A0B4K8A6;Q9W288
#> 71 Q5LJQ4;A0A0B4KEH8;A0A0B4KEC2;Q9W5H8
#> 72 A0A0B4KED0;Q9W5N2
#> 73 A0A0B4KED9;O16844
#> 74 A0A0B4KEE4;A1Z6Q1
#> 75 E1JGZ7;E1JGZ8;A1Z734;A0A0B4KEE7
#> 76 A0A0B4KEI5;Q9V9K7
#> 77 Q7JVY0;A0A0B4KEU5;A0A0B4KEJ7
#> 78 A1Z9L2;A1Z9L0;A0A0B4KFX4;Q8T076;A0A0B4KEP1;A0A0B4LFC1;A0A0B4KFM5;A0A0B4KF25
#> 79 Q5U156;A0A0B4KER0;Q95RL2
#> 80 A0A0B4KET0;Q1LZ08
#> 81 A0A0B4KFU3;A0A0B4KG58;B7YZJ2;B7YZJ1;E1JH90;A0A0B4KET5;A0A0B4KFA4;E1JH91;A0A0B4KEY4;A1ZAU8-2;A1ZAU8-3;A1ZAU8;A0A0B4KEY6
#> 82 Q0E901;A0A0B4KFE6;A0A0B4KEW2
#> 83 A0A0B4KFR7;A0A0B4KEW6;Q7KLE5
#> 84 A0A0B4KEX0;A1ZAB5
#> 85 Q0E993;A0A0B4KF06
#> 86 A0A0B4KF46;Q8T0L3
#> 87 A0A0B4KG14;A0A0B4KF57;Q9VMY8
#> 88 Q7JQL5;A0A0B4KF86
#> 89 Q8T0M2;Q0E9C6;A0A0B4KFA3;A8DY97;A8DY98
#> 90 Q9VHX9;A0A0B4KFA6
#> 91 A0A0B4LGR1;Q9VI14;A0A0B4KFB8;Q6NN86
#> 92 A1Z7H3;Q8T3L1;A1Z7H2;A0A0B4KFE4
#> 93 A0A0B4KFE5;Q04448-2;Q04448
#> 94 A0A0B4KFE9;A1Z8P9
#> 95 A0A0B4KGE6;A0A0B4KFH4;P26270
#> 96 A0A0B4KFJ7;Q9VHH9
#> 97 A0A0B4KFN1;A1Z9R6;A0A0B4KFX9;Q9V727
#> 98 A0A0B4KH36;A0A0B4KFQ0;A0A0B4KGR9;Q9VH01;A0A0B4KG50
#> 99 A4UZI0;A0A0B4LGK5;A1ZA18;A0A0B4KFR5;A0A0B4KG24
#> 100 A0A0B4KFX5;A0A0B4KGG9;A4V2S3;A0A0B4KHB2;A0A0B4KFT4;A0A0B4KGZ7;O46036-2;O46036
#> 101 A0A0B4KFU5;Q9V853
#> 102 A0A0B4KFW0;Q8T0S6
#> 103 Q9VHC4;A0A0B4KFZ2;Q6AWD5
#> 104 A0A0B4KFZ9;P84040
#> 105 Q7K0G4;A0A0B4KG11;F0JAK5
#> 106 A0A0B4KG32;A0A0B4KH26;Q9VH20
#> 107 A0A0B4KG41;Q9VES1
#> 108 Q9VF92;A0A0B4KG69
#> 109 Q9N6D7;A0A0B4KG96
#> 110 A0A0B4KHS7;A0A0B4KGE1;Q24151;A0A0B4KGI7;Q24151-2;A0A0B4KHS6;A0A0B4KH10;Q24151-4;Q24151-3
#> 111 Q8MQJ5;A0A0B4KGF5;Q9VE69
#> 112 Q32KD3;Q7KSW1;Q494I1;A0A0B4KGS8;Q9VHW9;A0A0B4KGF6
#> 113 A4V364;A8JR54;Q8IN47;A0A0B4KGK8;Q8IN48;A0A0B4KH21;A0A0B4KH24;A0A0B4KGF9;Q9VDI8;Q7KSA0;A0A0B4KHH8;A0A0B4KHI4;Q95TW4;A0A0B4KGK5;A0A0B4KHT5
#> 114 E1JIR4;A0A0B4KGG8;P13607-7;P13607-6;P13607-2;P13607-4;P13607-5;P13607;P13607-3;A8QI34
#> 115 A0A0B4KGH0;A0A0B4KHR4;Q9VDW6-2;Q9VDW6-1;Q9VDW6;Q9VDW6-4;Q9VDW6-3;A0A0B4KGB9;Q9VDW3;A0A0B4KHE2;Q7YU29;Q0KI50
#> 116 A0A0B4KGI6;Q9VN82;A0A0B4KG43;Q8IPP4;Q8IPP3;A0A0B4KF82;A0A0B4KFK9
#> 117 A0A0B4KGJ5;Q9NIV1;A0A0B4KG56
#> 118 A0A0B4KGK3;Q95RA8
#> 119 A0A0B4KGP8;Q24208;Q24208-2
#> 120 Q9VEV1;A0A0B4KGS4
#> 121 A0A0B4KGU4;Q9VHP0;M9PBB5;P09052
#> 122 A0A0B4KGW0;Q8IMX7-2;A0A0B4J3Z9;Q8IMX7
#> pval adj_pval diff t_statistic se df avg_abundance n_approx n_obs
#> 1 9.041054e-01 9.643171e-01 -0.13197309 -0.12175674 1.0839078 24 18.93537 12.00100 5
#> 2 9.228458e-01 9.643171e-01 -0.09926167 -0.09787319 1.0141865 24 18.44216 12.00100 1
#> 3 3.561254e-02 2.647212e-01 -2.91628269 -2.22664829 1.3097186 24 19.25697 19.27983 14
#> 4 6.674303e-01 9.643171e-01 0.63210212 0.43502624 1.4530207 24 18.71535 12.00100 6
#> 5 9.189871e-01 9.643171e-01 0.06891434 0.10278570 0.6704662 24 19.99188 17.39307 17
#> 6 9.226888e-01 9.643171e-01 -0.09951655 -0.09807306 1.0147186 24 18.50970 12.00100 1
#> 7 9.229678e-01 9.643171e-01 -0.09906384 -0.09771790 1.0137737 24 18.42516 12.00100 1
#> 8 6.434555e-01 9.643171e-01 -0.19662994 -0.46878223 0.4194484 24 21.87309 28.92211 29
#> 9 2.948952e-01 8.608983e-01 1.94720060 1.07083423 1.8183959 24 18.72725 12.00100 4
#> 10 5.977712e-01 9.643171e-01 -0.78261866 -0.53470805 1.4636373 24 18.96533 12.00100 4
#> 11 4.180174e-01 9.643171e-01 1.06811244 0.82406468 1.2961512 24 18.69294 12.00100 7
#> 12 5.444283e-01 9.643171e-01 0.65459176 0.61486774 1.0646058 24 18.72351 13.26599 13
#> 13 2.131380e-01 7.247578e-01 -1.92931574 -1.27896523 1.5084974 24 21.94096 34.50696 34
#> 14 9.225138e-01 9.643171e-01 -0.09980085 -0.09829572 1.0153122 24 18.49506 12.00100 1
#> 15 5.677737e-01 9.643171e-01 -0.30681826 -0.57931712 0.5296206 24 23.11365 33.97973 34
#> 16 4.364242e-01 9.643171e-01 0.63853127 0.79146721 0.8067691 24 21.83207 29.09390 29
#> 17 5.513705e-01 9.643171e-01 -0.92548437 -0.60421453 1.5317149 24 18.76627 21.16573 17
#> 18 1.265250e-01 5.322777e-01 -1.44866342 -1.58294091 0.9151721 24 18.76068 14.58983 13
#> 19 9.232499e-01 9.643171e-01 -0.09860718 -0.09735891 1.0128213 24 18.43896 12.00100 1
#> 20 8.456488e-01 9.643171e-01 0.13751343 0.19679002 0.6987825 24 24.96475 34.87011 35
#> 21 3.890306e-01 9.593122e-01 -0.49601587 -0.87728286 0.5654002 24 19.62093 19.68847 19
#> 22 5.796524e-03 6.833745e-02 -3.03236583 -3.02866863 1.0012207 24 19.39205 14.13399 12
#> 23 7.940276e-01 9.643171e-01 0.53549900 0.26400794 2.0283443 24 19.52978 12.00100 9
#> 24 7.822569e-01 9.643171e-01 -0.29071971 -0.27949849 1.0401477 24 19.93328 13.52792 13
#> 25 5.813170e-03 6.833745e-02 -2.36743316 -3.02746517 0.7819853 24 19.70369 17.49006 17
#> 26 7.660945e-04 2.710675e-02 1.31591990 3.85155010 0.3416598 24 22.63306 31.78235 32
#> 27 5.272829e-01 9.643171e-01 -0.39004152 -0.64149148 0.6080229 24 20.49255 23.49625 23
#> 28 2.138630e-01 7.247578e-01 -1.08737737 -1.27687450 0.8515930 24 21.40463 28.98317 29
#> 29 7.362019e-01 9.643171e-01 -0.34931409 -0.34082366 1.0249115 24 18.44341 12.00100 1
#> 30 2.927058e-01 8.608983e-01 1.36822590 1.07581648 1.2718023 24 18.76668 12.00100 4
#> 31 3.864093e-01 9.593122e-01 0.61668223 0.88221913 0.6990125 24 24.31247 36.00000 36
#> 32 8.433075e-01 9.643171e-01 0.28664737 0.19981653 1.4345529 24 18.54707 12.00100 2
#> 33 9.228504e-01 9.643171e-01 -0.09925422 -0.09786734 1.0141710 24 18.48510 12.00100 1
#> 34 2.977740e-01 8.608983e-01 -0.38453818 -1.06432295 0.3612984 24 21.23648 22.56518 23
#> 35 6.009883e-01 9.643171e-01 0.22887460 0.52998994 0.4318471 24 21.24522 27.52419 29
#> 36 9.181121e-01 9.643171e-01 -0.10707848 -0.10390000 1.0305917 24 18.56855 12.00100 1
#> 37 1.492533e-01 6.069632e-01 -1.68691214 -1.48998782 1.1321651 24 18.55429 12.00100 1
#> 38 4.587328e-02 2.647212e-01 1.14516920 2.10574906 0.5438298 24 28.10487 36.00000 36
#> 39 3.163508e-03 6.432467e-02 1.94489788 3.27986039 0.5929819 24 23.81095 34.14228 34
#> 40 2.233232e-02 1.816362e-01 3.30063096 2.44234451 1.3514191 24 19.57507 11.40295 10
#> 41 6.159690e-01 9.643171e-01 0.68682472 0.50817629 1.3515481 24 18.49667 12.00100 2
#> 42 9.081067e-01 9.643171e-01 -0.12457335 -0.11665170 1.0679086 24 18.56211 12.00100 1
#> 43 4.409985e-01 9.643171e-01 1.20409501 0.78349841 1.5368187 24 18.31312 12.00100 1
#> 44 9.151516e-03 9.304041e-02 -2.30696320 -2.83503908 0.8137324 24 20.17084 17.64724 17
#> 45 7.886930e-01 9.643171e-01 0.06831714 0.27102003 0.2520741 24 20.00811 22.13184 22
#> 46 4.954627e-01 9.643171e-01 -0.18675522 -0.69218740 0.2698044 24 19.82606 20.21045 20
#> 47 5.476326e-01 9.643171e-01 -0.44500254 -0.60994169 0.7295821 24 22.27409 32.25299 32
#> 48 9.186813e-01 9.643171e-01 -0.10612366 -0.10317509 1.0285783 24 18.41575 12.00100 0
#> 49 8.845945e-02 4.150789e-01 1.52566425 1.77573561 0.8591731 24 19.81764 16.28860 15
#> 50 7.816759e-01 9.643171e-01 -0.12516567 -0.28026492 0.4465977 24 22.00212 33.14310 33
#> 51 9.793620e-01 9.793620e-01 -0.03221180 -0.02613976 1.2322914 24 18.41672 12.00100 1
#> 52 2.214043e-08 2.701132e-06 4.37565997 8.16099836 0.5361672 24 27.33514 36.00000 36
#> 53 3.644474e-01 9.593122e-01 -0.80732733 -0.92446356 0.8732928 24 22.35185 29.01701 29
#> 54 3.876274e-02 2.647212e-01 -3.39268355 -2.18650755 1.5516450 24 19.17257 12.00100 7
#> 55 3.757219e-01 9.593122e-01 1.16676903 0.90257401 1.2927129 24 18.93425 12.00100 6
#> 56 6.408596e-02 3.257703e-01 -1.22481842 -1.94103583 0.6310128 24 23.05049 33.88476 34
#> 57 1.590711e-01 6.260217e-01 1.53028107 1.45337664 1.0529143 24 19.66376 17.13504 17
#> 58 1.131192e-01 5.111311e-01 -1.15443889 -1.64445458 0.7020193 24 18.99606 12.36380 12
#> 59 8.171631e-01 9.643171e-01 -0.09962472 -0.23374783 0.4262060 24 19.61498 18.37912 18
#> 60 1.066650e-02 1.001010e-01 1.19360307 2.76910017 0.4310437 24 21.05399 19.91169 21
#> 61 5.466287e-01 9.643171e-01 1.17432662 0.61148338 1.9204555 24 18.70086 12.00100 2
#> 62 7.919738e-01 9.643171e-01 0.13105252 0.26670600 0.4913745 24 19.78741 18.66593 18
#> 63 5.057939e-01 9.643171e-01 1.14337132 0.67553404 1.6925444 24 19.26095 12.28946 8
#> 64 3.145789e-01 8.722416e-01 -0.56927461 -1.02717720 0.5542127 24 23.37249 28.86215 31
#> 65 9.197907e-01 9.643171e-01 -0.10427451 -0.10176237 1.0246863 24 18.53550 12.00100 2
#> 66 9.083037e-01 9.643171e-01 0.13467183 0.11640049 1.1569697 24 18.41111 12.00100 5
#> 67 9.671411e-01 9.751340e-01 -0.02481156 -0.04162617 0.5960568 24 22.46840 31.86834 32
#> 68 6.861313e-01 9.643171e-01 -0.48243024 -0.40904871 1.1793956 24 18.45434 12.00100 1
#> 69 5.908034e-01 9.643171e-01 -0.16493733 -0.54496937 0.3026543 24 22.89392 27.59466 29
#> 70 5.766823e-01 9.643171e-01 0.71923197 0.56594920 1.2708419 24 18.35385 12.00100 1
#> 71 9.227639e-01 9.643171e-01 -0.09939453 -0.09797740 1.0144638 24 18.53772 12.00100 2
#> 72 9.206463e-01 9.643171e-01 -0.10285901 -0.10067301 1.0217138 24 18.47949 12.00100 1
#> 73 9.406044e-01 9.643171e-01 -0.05427922 -0.07529465 0.7208909 24 19.99532 14.41933 16
#> 74 7.009700e-01 9.643171e-01 -0.45739794 -0.38863842 1.1769241 24 18.69750 12.00100 5
#> 75 6.332662e-01 9.643171e-01 0.68952793 0.48329505 1.4267225 24 18.86672 12.00100 7
#> 76 5.034613e-01 9.643171e-01 -0.78512326 -0.67927729 1.1558214 24 18.47957 12.00100 1
#> 77 4.086408e-02 2.647212e-01 -2.43952580 -2.16134050 1.1287096 24 19.52318 11.50015 10
#> 78 9.553710e-01 9.712939e-01 -0.02783767 -0.05655103 0.4922575 24 19.40221 18.49791 18
#> 79 2.643095e-01 8.485727e-01 -0.82707846 -1.14300801 0.7235981 24 20.34291 19.45324 19
#> 80 3.034314e-01 8.608983e-01 1.16286378 1.05165640 1.1057450 24 19.37861 12.99106 13
#> 81 6.460869e-01 9.643171e-01 0.29912727 0.46505093 0.6432140 24 20.93932 24.48471 26
#> 82 9.246688e-01 9.643171e-01 -0.09632425 -0.09555318 1.0080696 24 18.49860 12.00100 6
#> 83 9.219635e-01 9.643171e-01 -0.10069764 -0.09899623 1.0171865 24 18.51485 12.00100 1
#> 84 3.931608e-01 9.593122e-01 -0.30146312 -0.86954862 0.3466892 24 24.03786 34.95610 35
#> 85 8.909985e-01 9.643171e-01 -0.15418119 -0.13850296 1.1131978 24 21.03032 25.94325 25
#> 86 6.161573e-03 6.833745e-02 -3.12259785 -3.00300548 1.0398242 24 21.28131 28.61920 28
#> 87 5.662968e-01 9.643171e-01 0.24855823 0.58154351 0.4274112 24 20.65478 23.37489 24
#> 88 2.860154e-01 8.608983e-01 1.38672126 1.09120856 1.2708123 24 19.09672 12.00100 7
#> 89 2.012315e-01 7.247578e-01 2.52039510 1.31410981 1.9179486 24 18.63057 12.00100 3
#> 90 2.369339e-01 7.812416e-01 1.21140104 1.21300108 0.9986809 24 20.50976 16.73872 16
#> 91 9.256282e-01 9.643171e-01 -0.09479415 -0.09433248 1.0048941 24 18.55994 12.00100 7
#> 92 8.887460e-04 2.710675e-02 -2.48594417 -3.79244092 0.6554998 24 19.83720 17.03640 17
#> 93 9.224449e-01 9.643171e-01 -0.09991298 -0.09838347 1.0155464 24 18.33192 12.00100 1
#> 94 4.582331e-02 2.647212e-01 -2.68606602 -2.10627611 1.2752678 24 18.86580 12.00100 3
#> 95 2.230302e-03 5.441937e-02 -3.91939652 -3.42256483 1.1451636 24 19.05694 12.00100 8
#> 96 4.878551e-01 9.643171e-01 0.29259449 0.70457684 0.4152769 24 19.05484 14.25221 14
#> 97 9.227330e-01 9.643171e-01 -0.09944476 -0.09801679 1.0145687 24 18.38561 12.00100 1
#> 98 1.782027e-02 1.552909e-01 -1.79833541 -2.54385073 0.7069343 24 20.02498 15.88401 16
#> 99 5.901771e-02 3.130505e-01 0.83306672 1.98221179 0.4202713 24 21.13012 25.95821 26
#> 100 4.550496e-03 6.833745e-02 -1.84444394 -3.12973639 0.5893288 24 19.56241 18.97891 18
#> 101 9.357241e-01 9.643171e-01 -0.13285593 -0.08149505 1.6302333 24 19.71583 10.50293 11
#> 102 3.463236e-01 9.389217e-01 0.31169419 0.96061703 0.3244729 24 20.53835 25.39201 25
#> 103 1.262833e-01 5.322777e-01 2.28575527 1.58400097 1.4430264 24 19.16008 12.00100 5
#> 104 6.925939e-01 9.643171e-01 0.42254441 0.40013843 1.0559956 24 20.63359 27.96731 27
#> 105 9.226612e-01 9.643171e-01 -0.09956140 -0.09810820 1.0148122 24 18.36957 12.00100 1
#> 106 8.580194e-01 9.643171e-01 -0.15295408 -0.18083004 0.8458444 24 18.97029 11.49544 11
#> 107 9.229830e-01 9.643171e-01 -0.09903924 -0.09769858 1.0137224 24 18.45665 12.00100 1
#> 108 6.273476e-01 9.643171e-01 0.66626468 0.49177315 1.3548212 24 18.56544 12.00100 2
#> 109 7.995168e-02 3.901642e-01 -0.45962634 -1.82836344 0.2513867 24 20.59743 23.14033 23
#> 110 4.773661e-02 2.647212e-01 -0.82728014 -2.08645261 0.3965008 24 22.16902 31.04219 31
#> 111 4.555582e-02 2.647212e-01 -1.34306297 -2.10910636 0.6367924 24 19.23886 14.40934 14
#> 112 2.137807e-01 7.247578e-01 0.46126776 1.27711141 0.3611805 24 20.58297 25.49768 25
#> 113 1.849850e-01 7.052554e-01 -1.54457675 -1.36477003 1.1317487 24 18.54254 12.00100 1
#> 114 5.582864e-01 9.643171e-01 -0.39746200 -0.59367135 0.6694984 24 22.07904 32.35369 32
#> 115 8.928653e-01 9.643171e-01 -0.15414526 -0.13611550 1.1324592 24 18.62768 12.00100 1
#> 116 2.088060e-04 1.273716e-02 6.30315637 4.36497128 1.4440316 24 20.30641 26.15976 24
#> 117 9.263544e-01 9.643171e-01 -0.09364303 -0.09340857 1.0025100 24 18.90580 12.00100 6
#> 118 4.478138e-01 9.643171e-01 -0.88731768 -0.77171825 1.1497949 24 18.48807 12.00100 1
#> 119 5.279699e-01 9.643171e-01 -0.46123120 -0.64041589 0.7202057 24 23.83053 31.57225 33
#> 120 5.993421e-03 6.833745e-02 0.83088692 3.01464062 0.2756172 24 22.26676 31.92679 32
#> 121 6.925957e-01 9.643171e-01 -0.26042810 -0.40013601 0.6508489 24 24.23721 36.00000 36
#> 122 9.227127e-01 9.643171e-01 -0.09947767 -0.09804258 1.0146374 24 18.55530 12.00100 1This walkthrough ends with the identification which proteins are differentially abundant. But for a real dataset, now the actual analysis only just begins. A list of significant proteins is hardly ever a publishable result, one often needs to make sense what the relevant underlying biological mechanisms are. But for this problem other tools are necessary, which depend on the precise question associated with the biological problem at hand.
Session Info
sessionInfo()
#> R version 3.6.1 (2019-07-05)
#> Platform: x86_64-apple-darwin15.6.0 (64-bit)
#> Running under: macOS Mojave 10.14.6
#>
#> Matrix products: default
#> BLAS: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRblas.0.dylib
#> LAPACK: /Library/Frameworks/R.framework/Versions/3.6/Resources/lib/libRlapack.dylib
#>
#> locale:
#> [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
#>
#> attached base packages:
#> [1] stats graphics grDevices utils datasets methods base
#>
#> other attached packages:
#> [1] proDA_0.99.10 BiocStyle_2.12.0
#>
#> loaded via a namespace (and not attached):
#> [1] SummarizedExperiment_1.14.0 xfun_0.8 lattice_0.20-38
#> [4] colorspace_1.4-1 htmltools_0.3.6 stats4_3.6.1
#> [7] yaml_2.2.0 rlang_0.4.0 pkgdown_1.3.0
#> [10] pillar_1.4.2 BiocParallel_1.18.0 BiocGenerics_0.30.0
#> [13] RColorBrewer_1.1-2 matrixStats_0.54.0 GenomeInfoDbData_1.2.1
#> [16] stringr_1.4.0 zlibbioc_1.30.0 munsell_0.5.0
#> [19] commonmark_1.7 gtable_0.3.0 memoise_1.1.0
#> [22] evaluate_0.14 Biobase_2.44.0 knitr_1.24
#> [25] IRanges_2.18.1 GenomeInfoDb_1.20.0 parallel_3.6.1
#> [28] Rcpp_1.0.2 backports_1.1.4 scales_1.0.0
#> [31] BiocManager_1.30.4 DelayedArray_0.10.0 S4Vectors_0.22.0
#> [34] desc_1.2.0 XVector_0.24.0 fs_1.3.1
#> [37] digest_0.6.20 stringi_1.4.3 bookdown_0.12
#> [40] GenomicRanges_1.36.0 rprojroot_1.3-2 grid_3.6.1
#> [43] tools_3.6.1 bitops_1.0-6 magrittr_1.5
#> [46] RCurl_1.95-4.12 tibble_2.1.3 crayon_1.3.4
#> [49] pkgconfig_2.0.2 MASS_7.3-51.4 pheatmap_1.0.12
#> [52] Matrix_1.2-17 xml2_1.2.0 assertthat_0.2.1
#> [55] rmarkdown_1.13 roxygen2_6.1.1 extraDistr_1.8.11
#> [58] rstudioapi_0.10 R6_2.4.0 compiler_3.6.1